ニューロンモデルの数式と最急降下法

さきほど、ニューロンモデルでは膜電位のしきい値によって、0と1の出力をあらわすことができると述べた。膜電位は、図2の（1）のようにあらわすことができ、階段関数をstep()とするとニューロンの出力yは図2の（2）のようになる。

ここで、バックプロパゲーション（BP）の基礎となる「最急降下法」について説明する。最急降下法とは、2乗誤差Eが小さくなる結合係数を求めるための方法の1つである。この方法では、誤差関数のある点での微係数（傾き）を求めて誤差Eが少なくなる方向へ結合係数Wを変化させていく。この様子を少し数式で展開しよう。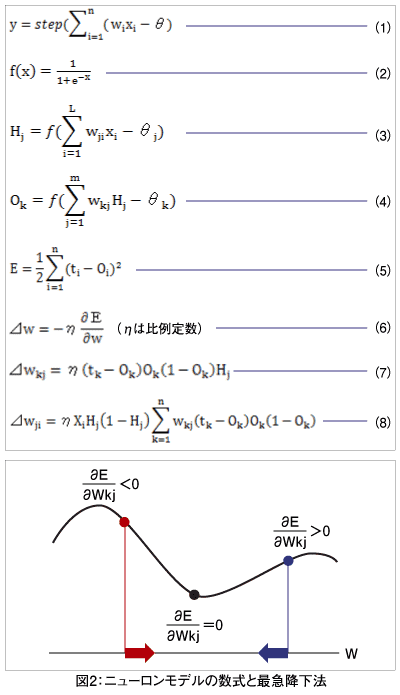

前向き演算（ニューロン出力の計算）と後向き演算（結合係数の修正）

前向き演算として、中間層、出力層の各ニューロンの出力を計算する。バックプロパゲーションを考案したRumelhartらは、ニューロンの出力関数fとして階段状関数ではなく、微分可能な関数としてシグモイド関数（3）を導入している。

その時の、中間層ニューロンjの出力H_jは、図2の（4）となる。ゆえに出力層ニューロンkの出力O_kは、図2の（5）となる。

ここで、x_iは入力層のi番目のニューロンへの入力（入力層では入力＝出力）、w_jiは入力層と中間層の間の結合係数、w_kjは中間層と出力層の間の結合係数、θ_jは中間層ニューロンjの発火しきい値、θ_kは出力層ニューロンkの発火しきい値となる。

次に、後向き演算（結合係数の修正）について解説する。2乗誤差Eは、図2の（6）のようにあらわすことができる。

バックプロパゲーションでは、この2乗誤差Eを小さくなるように結合係数を修正する。したがって結合係数の修正量は、2乗誤差Eを結合係数で偏微分して、2乗誤差Eの結合係数に対する微係数（傾き）が正（右上がり）であれば、結合係数は小さくする。また、微係数（傾き）が負（右下がり）であれば、結合係数は大きくする。したがって、微係数（傾き）と修正量の符号は逆になる。微係数（傾き）がゼロになると修正量もゼロとする。したがって、修正量は図2の（7）のようになる。

Rumelhartらは、ニューロンの出力関数としてシグモイド関数を導入したのだが、これは階段状関数では結合係数に対して偏微分できないため、階段状関数に近いが微分可能な連続関数をニューロンの出力関数とするためであった。

2乗誤差Eの結合重みに対する偏微分が求められることから、結合係数を修正して誤差を減少させる後向き演算ができるようになる。修正量ΔWkjを詳しく表すと図2の（8）となる。

ここで、t_kは出力層のk番目のニューロンの教師信号、O_kは前向き演算で得られた出力層のk番目のニューロンの出力値、H_jは前向き演算で得られた中間層のj番目のニューロンの出力値となる。

このようにして、中間層と出力層の間の結合係数の修正量ΔWkjを求めることができる。さらに、入力層と中間層の間の結合係数の修正量ΔWjiは、図2の（9）となる。ここで、X_iは入力層のi番目のニューロンへの入力（入力層では入力＝出力）である。

このようにして、入力層と中間層の間の結合係数の修正量ΔWjiを求めることができる。

結合係数の修正量の導出など、バックプロパゲーションに関する詳しい内容は筆者らが用意した「ニューラルネットワーク入門（http://
www-ailab.elcom.nitech.ac.jp/lecture/neuro/）」を参照していただきたい。 次のページ