パルスニューロンモデルのハードウェア化

先にも述べたように、階層型ニューラルネットワークで用いるモデル化では、ニューロンの膜電位と結合係数は連続数値、さらにはシグモイド関数の出力も0から1の間の連続数値であり、これらを整数型あるいは浮動小数点型の複数ビットを用いてデータ表現をしている。

このため、ニューロンの膜電位と結合係数の乗算には乗算器を必要とする。したがって、階層型ニューラルネットワークでは、高速演算器を有したコンピュータを用いて、プログラムで記述されたデータ演算を繰り返すことを想定しており、ハードウェア化には適していない。

これに対して、パルスニューロンモデルはより生体の神経細胞の情報伝達機構に近く、ニューロンの入力・出力信号は時系列的なパルス列（0と1の1ビット時系列信号）で表わされ、局所膜電位も生体を模した減衰関数を用いている。

パルスニューロンモデルでは入力値が0か1であるため、入力値と結合係数の乗算を積算ではなく、入力値＝1が入力された時に結合係数の値を出力するAND回路で実現することができる。

AND回路は積算器に比べて回路規模が小さく、さらに1つのAND回路をニューロンのシナプス数だけ、順番に繰り返し使うことで従来のニューロンモデルに比べて非常に小さい回路規模で実装することができる。AND回路より出力されたそれぞれの値は加算器を用いて累積加算され、比較器でしきい値と比較して出力が決定される。

筆者らは、任意のディジタル回路をVHDL（VHSIC Hardware Description Language）などのハードウェア記述言語で設計し、外部から何回も書き込むことができるフィールドプログラマブルゲートアレイ（FPGA）を用いて、ニューラルネットワークを実現している。

ハードウェア化されたパルスニューロンモデルのブロック図を図2に示す。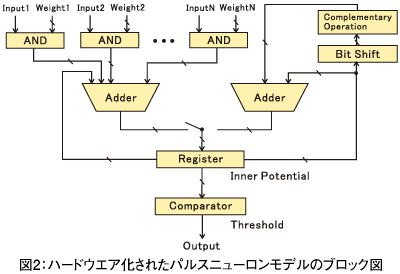

パルスニューロンモデルにおける演算について

時定数による減衰は、ビットシフトと補数演算で実現しており内部電位の何分の一かを減算するという演算を行う。

本来、減衰時定位数はシナプスの局所膜電位ごとに用意するものであるが、本実験では各局所膜電位の時定数を同じ値としたため、局所膜電位の総和である内部電位に対して減衰を持たせることで等価な回路とした。

なお、今回の実装にあたってはパルスニューロンモデルの持つ学習機構はFPGA上に実装されていない。このため、計算機上であらかじめ学習して生成された結合係数を固定小数点表現に変換して回路に与えており、FPGAでは認識動作のみを行うこととしている。

時間差検出ネットワークでは、パルス情報を移動させるためのシフト演算器とパルスニューロンモデルを横一列に配置することで実装する。 次のページ