図解！二分探索のプログラミング

二分木（Binary Tree）

　「第1回：サーチのアルゴリズムを学ぶ」は、動的に増減する要素をリンクトリストで管理する方法を紹介しました。

　リンクトリストでは要素を探索する場合、リンク（ポインタ）を順にたどるしかないため、線形探索と等しい時間がかかってしまいます。今回は、リストと同様にポインタでつながった構造でありながら、探索時間は二分探索と同じ性能の構造である二分木（Binary Tree）を紹介します。これはB-Tree や Balanced Tree（バランス木）と言葉も機能も似ていますが、少し違います。今回は、探索目的に使う二分木である二分探索木（Binary Search Tree）と呼ぶものを扱います。

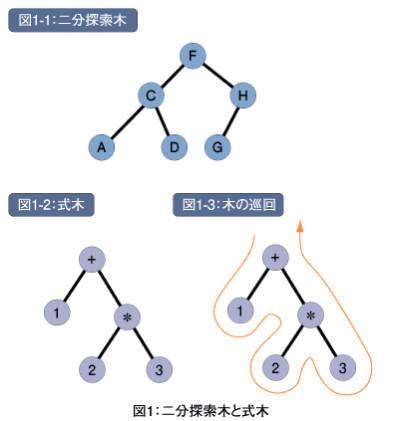
　図1-1に二分探索木を示します。

　全体を木だと思ってください。丸をノード（node；節）と呼びます。また、ノードから出ている線は木の枝（branch）に相当します。各ノードから多くても2本の枝が出ているので二分木と言います。枝は1本だけでも構いませんし、枝を持たないノードがあっても構いません。枝を持たないものを葉（leaf）と呼びます。一番上のノードが根（root）です。

　根は木の場合は一番下にあるのが普通ですが、このようなツリー構造の場合は根を上に書くのが普通です。丸の中に書いてあるのは、そのノードの名前ですが検索の場合の「キー」に相当します。

　先に進む前に、木を「歩く」練習をしましょう。「木を歩く」とは変な言い方ですが、すべてのノードをたどる作業です。Tree Traversalまたはwalkと言います。

　わかりやすくするために数式を木構造で表現したものを考えます。

1 + 2 * 3

　これを式木（expression tree）として表現すると図1-2のようになります。

　この木を巡回するわけですが、図1-3のように左側からぐるっとまわることを想像してください。そして、通ったノードをすべて印字するのですが、どのタイミングで印字したらよいでしょう？

　これには3つのやり方があります。あるノードとその下の左右の木を印刷するとして、今着目しているノードが「自分」だとすると、以下の3つが考えられます。

（1）出くわしたノードの順に印字する
（2）自分の左側の部分木を印字して、自分を印字して、右側の部分木を印字する
（3）自分の左側の部分木を印字して、右側の部分木を印字して、自分を印字する

　それぞれの方法で上の式木を印字すると次のようになります。

（1）+ 1 * 2 3
（2）1 + 2 * 3
（3）1 2 3 * +

　（2）は元の数式と同じになりますが、これは式の表現方法のうちの「中置記法」（infix notation）と呼ばれるものです。（1）は「前置記法」（prefix notation）、（3）は「後置記法」（postfix notation）です。

　（1）は別名、ポーランド記法（polish notation）、（3）は逆ポーランド記法とも呼ばれます（しかし、歴史的にはこうなのですが、（3）を「ポーランド」（1）を「逆ポーランド」と呼ぶのが一般的のようです）。

　木構造を探索するということは、最も単純にするならば、歩き方は上のどれでも構いませんがすべてのノードを調べることです。出くわしたノードのキーと目的のキーとを比較して一致すればそれがターゲットです。配列やリストの線形探索と同じで「総当たり」するわけです。ただ、これでは時間がかかります。そこで二分木の登場というわけです。

二分探索木の登場

　図1-1を再度見てください。これがなぜ「探索木」なのかと言えば、ノードのキーがソートされているからです。

　「ソートされている」ことは、「あるノードを見たとき、その左側にある部分木に含まれるすべてのノードのキーは、はじめのノードのキーよりも小さい」「あるノードを見たとき、その右側にある部分木に含まれるすべてのノードのキーは、はじめのノードのキーよりも大きい」ことを表します。

　値が等しいときの扱いは別に決めますが、ここでは簡単にするために同じキーはないと考えましょう。

　図1-1では、根に「F」がありますが、左の部分木には「A」「C」「D」があり、いずれも「F」よりも小さいものです。右側には「F」よりも大きいものだけがあります。

　では、続いてこれをPHPで考えてみましょう。