ソースでわかる！ハッシング

衝突の回避（2）：置き場の調整

　衝突が起こったときのための別の作戦を立てましょう。データを登録する際に、すでに同じハッシュ値を持っているデータが存在していると、配列のその場所は埋まっていることになります。この場合にどうすればよいでしょう？

　ひとつの方法は、「その近くに空きを探す」というものです。

　これは、新しくデータを挿入するときの作戦です。逆にデータを探す際には、ハッシュ値から得られるインデックスの場所に狙いのものがなかった場合でも、「その近辺を探す」ことを意味します。

　「近くを探す」と言うとあいまいな言い方ですが、具体的にはインデックスがひとつ小さいところを探してそこが空いていればそこに入れる。そこも埋まっていればさらにそれより小さいところを探す、というものです。

　一見するとあまりエレガントな方法には見えないかもしれませんが、それでも総当たりするよりは検索の範囲が狭まります。この方法についてはこれ以上は踏み込みませんが、登録するデータに上限がある場合には十分有効な手段です。

衝突の回避（3）：リンクトリストとのコラボ！

　ハッシュ関数をどれほど調整しても衝突は回避できません。また、われわれのデータの置き場（一定のサイズの配列）では、サイズを超えたデータが現れれば、必ず衝突は起こります。このシリーズは増減するデータに対する検索がテーマですから、データ件数の上限を決めてしまいたくはありません。その上限を十分大きくとることで対応することも可能ですが、それでも固定的な配列では常に限界を持つことになります。

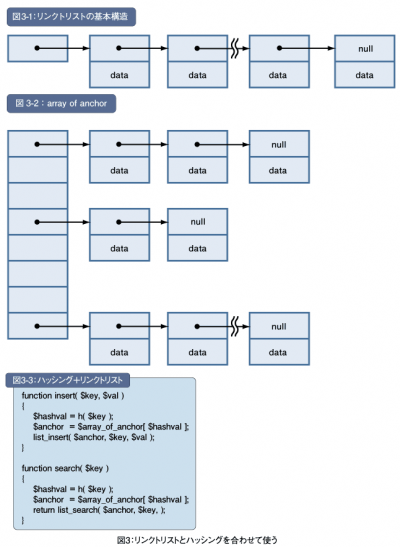
　それで、これまでに紹介した方法との併せ技を使います。図3-1は「第1回：サーチのアルゴリズムを学ぶ（http://www.thinkit.co.jp/article/159/1/）」で紹介したリンクトリストです。

　このデータ構造では、データの増減には対応できるものの、データの検索が線形探索になるので、時間がかかることが問題でした。

　リンクトリストで問題なのは、リストが長くなることです。長くなれば長くなるほど検索のための平均探索時間が延びます。そこで、短いリストをたくさん作ったらどうでしょう。短いリストを探索するのであれば、時間はさほど気になりません。

　今回のハッシングでは衝突が問題になりました。そこで、リンクトリストの問題点とハッシングの問題点を併せて解決しましょう。つまり、ハッシングを基本としながらも、衝突したものはリンクトリストで管理するのです。図3-2のようなイメージです。

　この図で左側に配列があります。これがハッシュ値に対応した配列です。その中身はリンクトリストへのポインタ、つまりアンカー（anchor）です。同じハッシュ値を持つものを1つのリンクトリストにつなげます。こうすることで衝突をいわば「吸収」します。

　単純なリンクトリストの場合にはアンカーが1つでした。それをハッシングと組み合わせます。アンカーを決めるためにハッシュ関数を使って配列のインデックスを求めます。これでアンカーが決まります。アンカーが決まれば、そこに連なるリンクトリストに対して追加／登録や削除、検索を実行します。

　リストの長さは単独の場合よりもはるかに短くなるでしょう。また、ここでもハッシュ関数の性能が重要なのですが、ハッシュ値ができるだけ分散するようにすることが、リストの長さを短くすることにつながります。

　第1回のinsert()とsearch()をそれぞれlist_insert()とlist_search()に置き換えれば、新しいinsert()とsearch()は図3-3のようになるでしょう。

　なかなかおしゃれだと思いませんか？このあたりの詳しいことは、プログラムとともに次回にご紹介しましょう。

　ハッシングの話はいろいろなところに出ていますが、執筆にあたって主に次のものを参考にしました。

Donald E.Knuth『The Art of Computer Programming, Vol III. 2nd ed.』McGraw-Hill（発行年：1998）