Prologと宣言型プログラミング
Prologと宣言型プログラミング
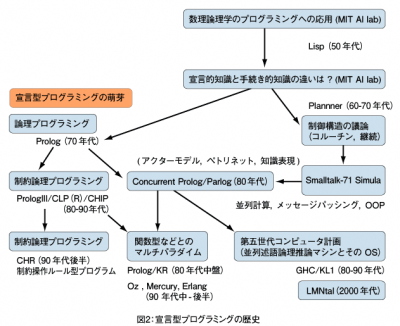
本連載では、Prologを、単なる一プログラミング言語仕様としてではなく、宣言型プログラミングの象徴として扱います。Prologは、当初は論理型プログラミング言語として開発されましたが、その後はさまざまな研究成果を取り込み、宣言型パラダイムの実験場のような言語へと変化してきているからです(図2)。
Prologプログラムは、問題を解くための手続きではなく、問題間の関係を記述します。関係は「述語(引数, ...)」という形式で、述語の定義によって記述されます。述語は関数に似ていますが、真か偽かのいずれかの値のみを取るという点が異なります。
述語の引数には、数値やシンボルなどの定数や、それらを組み合わせた項やリストなどのさまざまなパターンをリテラル記述することができます。これこそが、Prologプログラムが「宣言的」と言われる理由です。宣言的なパターンのマッチングによる探索が、Prologの根幹を成すメカニズムとなります。
確定節と証明による計算メカニズム
例えば、花子は太郎を好きであるという述語は「好き(花子,太郎).」と書けます。最も単純なPrologプログラムは、このように具体的な事実を書き並べたものとなります。変数を使うと、より一般的な「好き(花子,X).」のような述語が書け、Xが花子が好きな人ならば真、それ以外は偽という定義が記述できます。
その際に「花子は身長180cm以上の男子が好きである」というより複雑な条件については、「好き(花子, X) :- 男(X), 身長(X, Y), Y >= 180.」と記述することができます。このような特別な形の論理式のことを、確定節と呼びます。先に述べた具体的な事実は、ほかに条件が存在せず、無条件に真(しん)なので「:-」の右側を省略した確定節です。
もちろん、単に論理式を記述しただけでは、そこからどのような帰結が得られるのかは簡単にはわかりません。Prologは、確定節という扱いやすい形で論理式を記述し、SLD(Selective Linear Resolution for Definite Clause)導出というアルゴリズムで証明を行います。ここで言う証明というのは、通常の数学の証明とは異なり、条件を満たす具体例を実際に作って示すことです。
先の例で言うと、「『花子はXを好き』という述語を満たす具体例を作るためには、男子であり、身長Yが180以上という条件を満たすXを、事実の定義の中からしらみつぶしに探せば良い」という風に、述語の宣言的な記述を、手続きとして読み替えることによって、論理式を実行することが可能になります。このような宣言の手続き的解釈こそが、論理によるプログラミングの基本を成すアイデアと言えます。
このようにPrologプログラムには、直接問題の解法を書かなくても、問題に関する事実や関係を書き並べていくだけで、自動的に言語処理系が解答を探し出してくれるという、ほかのプログラミング言語とは決定的に異なる特徴が生まれます。これはすなわち、開発したいソフトウエアの仕様記述自体を動かして動作を確かめることができるという、画期的なアイデアであると言えます。
プログラミングの際、実は一番難しいのは、プログラムを書くことではなく、解くべき問題の仕様をはっきりさせることだと言えます。問題の仕様さえ明確な形で記述できれば、後はその仕様を直接SLD導出などのアルゴリズムで実行し、「仕様のデバッグ」を行うことができるというのが、宣言型パラダイムの最大の強みであると言えます。
- この記事のキーワード