探索(search)
探索(search)
さて、ソートについてはこれくらいにして、最後にサーチについて少し考えてみます。
サーチ(search:探索)とは、文字通りものを「探す」ことです。
データを集めておいてその中から目的のものを探し出すというのは、コンピュータの中では頻繁にある作業です。ですから、できるだけ効率よく探せなければいけません。
今、配列があって、その中にある数値を探すことを想定します。目的の数値が格納されているインデックスを求めるのがゴールです。
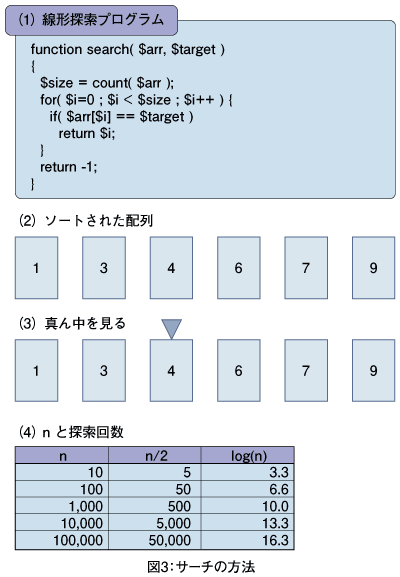
一番簡単な方法はリニアサーチ(線形探索)と呼ばれるものです。これは配列を端から順番に見ていきます。プログラムは図3のような感じになるでしょう。
簡単ですね。見つからなかったときにはあり得ないインデックス(-1)を返すことに注意してください。
考え方は簡単ですが、計算時間はどうでしょう?
n個の配列だとして、最善の場合はラッキーなことに1回の比較で目的のものが見つかるかもしれませんが、最悪の場合はn回の比較をすることが必要です。ですので、平均としてはn/2回ということになります。個数が倍になれば探索時間も倍になる、というわけです。
2分探索の方法
それではもう少し速い探索方法としてバイナリサーチ(2分探索)を紹介しましょう。図3の(2)を見てください。このように配列の中で数値がソートされていたとします。
このような場合でも線形探索を使うことができますが、それではまったくスピードアップになりません。このようなときには2分探索を使います。その考え方は次の通りです。
(1)まず、配列の真ん中(またはその1つ隣)の数値を見ます。
(2)目標の数値をこれと比較します。一致すればそれが目的のものです。
(3)一致しないとき、目標の数値が大きければ、それは今見ているところよりも右側にあるはずです。逆に小さければ、左側にあるはずです。
(4)そのようにして右側か左側というように、見る区間を半分に狭めていきます。
(5)最後には、目的のものに出くわすか、それとも見つからないかのどちらかです。
詳細は省きますが、この方法で目標物を見つけるまでの平均探索回数はlog(n)であることがわかっています。これがどれくらい速いかは図3(4)の比較表を見れば一目瞭然でしょう。データ件数が1,000件のとき、線形探索では平均500回の比較を行いますが、2分探索では約10回の比較で済みます。
こんな速い方法があるならすべて2分探索にしてしまえば良いのですが、この方法が使えるのはデータがソートされていることが前提条件です。結局、アルゴリズム(方法)は対象とするデータ構造に大きく依存することになります。アルゴリズムについての本が数多く出版されていますが、ほとんどが「データ構造とアルゴリズム」というようにセットで説明されているのも、それらが不可分のものだからなのです。
さて、5回にわたってアルゴリズムのほんの一端を見てきました。
「第1回:アルゴリズムからプログラムを学ぼう!(http://www.thinkit.co.jp/article/62/1/)」でも書きましたが、現代のプログラミング言語は多くのアルゴリズムをライブラリ関数として提供してくれます。ですから、このような基本的な機能を自分で作る機会も必要もほとんどないでしょう。
しかし、多くは定石と呼んでよいような基本的な考え方を勉強することで、より本質的なものの考え方を身につけることができます。そして、これらの定石を基礎として、現実のシステム設計を堅牢なものにすることができるのです。
今回紹介できませんでしたが、もちろんほかにもさまざまなアルゴリズムがあります。読者の方々が、これをきっかけに多少なりともソフトウェア工学に関心を持っていただければ、筆者の望外の幸せです。