重み係数にスパース性を仮定して多項式回帰をしてみよう!

はじめに

前回は「スパース性」について学びました。日本語に訳すと「疎」という意味を持つスパースですが、データ分析の界隈では「データの中にゼロ(もしくは、ほぼゼロ)が沢山ある」という様子を意味します。

私たちが扱うデータもしくは現象にはスパース性を持つものが少なくありません。その性質を逆手に取ることで、前回の記事で扱ったような、例えばノイズ除去といった応用技術に繋がります。今回はスパース性を考慮しながらデータを数式で捉える「スパースモデリング」という技術を概観していきます。

スパースモデリングとは

スパースモデリングを端的に説明するなら「解がスパースであると仮定して、問題を解く手法の総称」と言えます。スパースモデリングというアルゴリズムが存在するわけではありません。スパース性を意識しながら、データに潜む構造や入出力関係を数式で捉えるアプローチがスパースモデリングです。

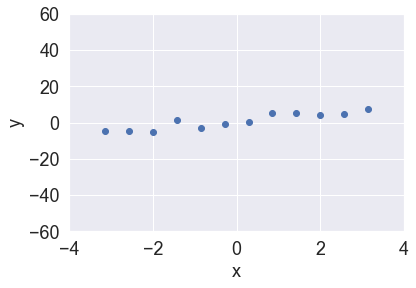
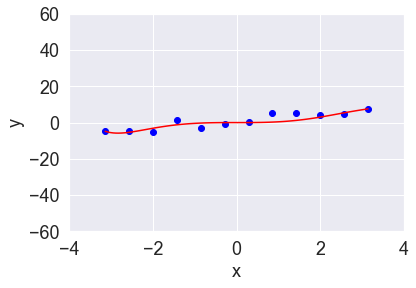
スパースモデリング「ではない」例を挙げてみます。図1のようなデータセットに対して、1変数の多項式回帰モデルを最小二乗法を用いて当てはめてみます。

図1：データ

説明変数と目的変数はそれぞれ$x$と$y$とします。回帰モデルは以下の関数$f(x;w)$設定します(あえて非常に高次の要素を含んだモデルを使っています)。

$$f(x;w) = \sum_{ i = 0 } ^ { 11 } w_i x^i$$

$w=(w_0,w_1,w_2, \cdots ,w_{11})$はモデルパラメータです。最小二乗法という枠組みでは、最適なモデルパラメータは以下の二乗誤差関数に最小値を与える$w$です(ここで$N$はデータ数を表わします)。

$$\frac{ 1 }{ 2 } \sum_{ n = 1 } ^ { N } ( y_n - f(x_n;w))^2$$

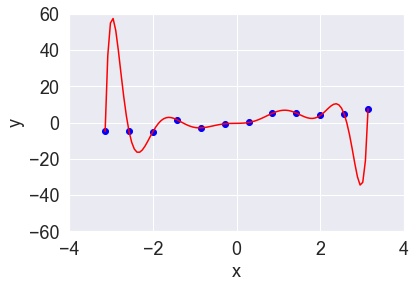
最小二乗法の考えは非常に単純です。目的変数$y_n$とモデルの出力$f(x_n;w)$の差の二乗がなるべく小さくなるような$w$を見つけよう、ということですね(二乗を取るのは、差を正の値に変換するためでした)。実際に上記の最適化問題を解き、回帰曲線を求めると図2のようになります。

図2：回帰曲線(多項式回帰)

この回帰曲線は、全データを通る曲線です。このような柔軟な曲線になるのは、モデルの中に$x^5$や$x^7$などの高次の要素が入っているためです。この回帰曲線は使い物になるでしょうか。

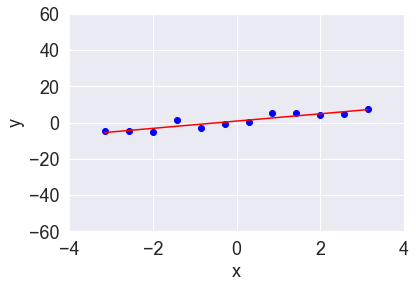
私達がほしい回帰曲線はもっとデータの傾向を捉えたものであるはずです。そこで、モデルパラメータ$w$にスパース性を仮定してみましょう。ここではまず、モデルに人為的にスパース性を取り込んでみます。$x$の0乗および1乗「以外」の全ての成分はほとんど$y$に寄与しないと仮定し、$x$の0乗および1乗「以外」にかかる重み係数の値を0.0001に設定して回帰させてみます。すると回帰曲線は図3のようになりました。

図3：人為的に重み係数をスパースにして回帰

データの大局的な動きを上手く捉えられていますように見えますね。これがスパース性を考慮するメリットの1つです。

L1、L2、L0正則化

先ほどは人為的に$x$の0乗および1乗「以外」にかかる重みを0に近づけました。この操作をアルゴリズムにより自動的に実施することを考えてみましょう。つまり「重み係数をスパースにしながら、二乗誤差関数を最小化する！」ということです。

まずは、スパース性という観点で重み係数の良し悪しを測る指標を作りましょう。モデルがスパースになるにはいくつかの重み係数が0(もしくはほぼゼロ)になる必要があります。みなさんは、どのような指標を思いつきますか。

様々なアイデアがあると思いますが、以下のような指標はどうでしょうか。

$$\begin{vmatrix} w_0 \end{vmatrix} + \begin{vmatrix} w_1 \end{vmatrix} + \begin{vmatrix} w_3 \end{vmatrix} + \cdots + \begin{vmatrix} w_{11} \end{vmatrix} = \sum_{ i = 0 }^ {11} w_i$$

重み係数の絶対値を取って、全て足し合わせたものです。それぞれの重み係数が0に近くなるほど、全体の値も小さくなるような設計となっています。二乗誤差関数も上記の指標も小さくなればなるほど良いので、それらを足し算して以下のような新しい最適化対象の関数を作ることにします(なお$α$は第1項と第2項の強さのバランスを調整する係数です。$α=0$のときに元の二乗誤差関数に戻ります)。

$$\frac{ 1 }{ N } \sum_{ n = i }^N ( y_n-f(x_n;w))^2 + α \sum_{ i = 0 }^ {11} \begin{vmatrix} w_i \end{vmatrix}$$

この関数を最小化すると、二乗誤差が小さく、さらに重み係数の絶対値の和も小さい、重み係数が求まります。最適化の結果、0(もしくはほぼゼロ)の重み係数が多くなるほど、モデルはスパースになります。

このように、元々の最適化対象の関数(今回は二乗誤差関数)に追加の項を付けることでパラメータに制約を与えることを正則化と言い、重み係数の絶対値の和で構成された項を加えることをL1正則化と言います。

先ほどは絶対値の和を使いましたが、「二乗の和」を用いてもスパースな$w$が期待できます。

$$w_{ 0 }^{ 2 } + w_{ 1 }^{ 2 } + w_{ 3 }^{ 2 } + \cdots + w_{ 11 }^{ 2 } = \sum_{ i = 0 }^ {11} w_{ i }^{ 2 }$$

こちらはL2正則化と呼ばれる手法です。L2正則化では、重み係数は0になるとは限らず、0に近い値に誘導されることが多いです。これはなぜでしょうか。二乗という操作がポイントです。例えば0.01という値を二乗すると0.0001というさらに小さな値になります。これにより重み係数を0にしなくても、関数全体を小さくするという目的を達成しやすいのです。

L1、L2という正則化が出てきましたが、最後に「0乗」の場合を考えてみましょう。

$$w_{ 0 }^{ 0 } + w_{ 1 }^{ 0 } + w_{ 3 }^{ 0 } + \cdots + w_{ 11 }^{ 0 } = \sum_{ i = 0 }^ {11} w_{ i }^{ 0 }$$

この項を付けた場合はL0正則化と呼ばれます。このでの0乗の定義は

$$w_{ i }^{ 0 } = \left\{ \begin{array}{ll} 1 & if & w \neq 0 \\ 0 & if & w = 0 \end{array} \right.$$

と定義されることが多いです。つまりL0正則化とは「0でない重み係数の個数(のα倍)を誤差関数に加える」という意味になります。実はこの最適化は少々面倒です。0乗の定義がルールベースであるため、微分という手段が使えません。「$w_0=0$の場合、$w_1=0$の場合、$w_2=0$の場合、…」というように、重み係数が0となる部分を先に定めて、各場合における最適化に取り組む必要があります。計算量が非常に多くなるため、実問題ではあまり利用されません。

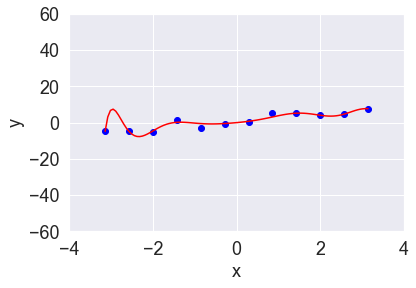
以下の図4、5はそれぞれ、図1のデータに対してL2正則化およびL１正則化を加えて多項式回帰をした結果です。少々曲がった部分がありますが、全体的には直線に近く、図2のような“飛び出した”動きが抑えられています。

図4：L2正則化(α=1)

図5：L1正則化(α=1)

スパースモデリングの応用例

現在スパースモデリングは、画像データに対する応用が非常に活発です。スパースモデリングはデータが比較的少数でも上手く機能することが分かっています。それはスパースモデリングが、データの中に含まれる重要な要素は多くない(＝スパースである)という立場でデータ分析するためです。

どうしても少数のデータしかとれないという事例は意外にも少なくなく、例えば、写真による製造品の欠陥判定の場面では、そもそも欠陥品が発生しない場合があります。深層学習は学習が上手く成功すると非常に精度の高いモデルを構築可能ですが、その分大量のデータが必要とされるため、分析に必要なデータ量という観点ではスパースモデリングに分があります。所持しているデータの量を考慮して深層学習とスパースモデリングを使い分けていくと、データ分析の幅を広げられるでしょう。

おわりに

今回で、本連載は最終回となります。全14回を通して機械学習・深層学習に関わる「数学」を学びました。まずは、空前のAIブームを捉え直した第1回。ディープラーニングの本体は実は「数学」であることをお伝えしました。ディープラーニングは数学という言語で設計され、プログラミングによってコンピュータ上に実装されています。

第2回以降は、数学の中でも微分と線形代数に着目。ニューラルネットワークの学習は微分が必要不可欠であること、線形代数の力を借りればビッグデータの取り扱いが格段に楽になることを学びました。線形代数の応用としては、非負値行列因子分解という手法を学びました。足し算的にデータを理解する性質を保つため、顔の画像に適用すると顔のパーツ(目や鼻など)を特徴として抽出できます。最後に「スパース」という性質を学びました。スパースモデリングは、ディープラーニングと並んで非常に注目されている技術です。ぜひこれからも動向をチェックしてみてください。

深層学習を含む機械学習では、数学に直面する場面が多々あります。これからさらに深く機械学習を学ぶ際には「今見ている数式が表現したいこと」を意識してみてください。ほとんどの数式には存在理由があります。特に機械学習のような応用形の分野ではその色が強いでしょう。「そもそもこの数式は、何を表現する(＝モデル化する)ために作られたのだろうか」「長い数式だが、いったいどの項が本質的に大事なのだろうか」。そういった心構えが数式と向き合うときには大切です。数式全体が重要であることもありますが、時には本質的に重要であるのは一部分であり、その他の部分は“上手くいくように付けられた脇役”程度の場合もありえます。

本連載が機械学習・深層学習を学ぶきっかけとなっていただければ、執筆者一同幸いです。機械学習は産業における必須の技術になりつつあり、ビジネス応用の例もますます増えています。ぜひ、是非これからも機械学習の世界を探求してください！