次元の扉 ー行列式と逆行列ー

次元の扉

あなたは3次元の世界に生きています。前後左右と上下がある世界です。今、目の前に3つの扉があります。2次元への扉、3次元への扉、そして4次元への扉です。

非常に興味深いですね。2次元の扉の先はきっと平面でしょう。3次元の世界は? 様子はきっと今と変わりませんが、一体どこに繋がっているのでしょうか。4次元の世界は…? 想像すらできませんね。

あなたはどの扉を開けるでしょうか。それとも…開けないでしょうか? それはもう戻れない気がするから? 人間とは不思議なもので、例えば洞窟に入ったとき、例えば深い森に入ったとき、いつも心配するのは「戻って来ることができるか」です。ただし今回ばかりは、その直感は正しいかもしれません。

行列式は逆行列の存在を決める

今回も、いきなり前回のように始めましたが、今回のテーマは「行列式」と「逆行列」です。行列式は、「正方行列に逆行列が存在するか?」という判断を下すための指標です。例えば、とある正方行列を$A$とすると、行列式は

$$detA もしくは |A|$$

と表記されます。detは「determinant」の略で、直訳すると「決定式」です。本記事では計算方法を解説しませんが、行列式を計算した結果がちょうど0となれば、その正方行列は逆行列を持ちません。行列式は逆行列が存在するかどうかを決定してくれるのですね。

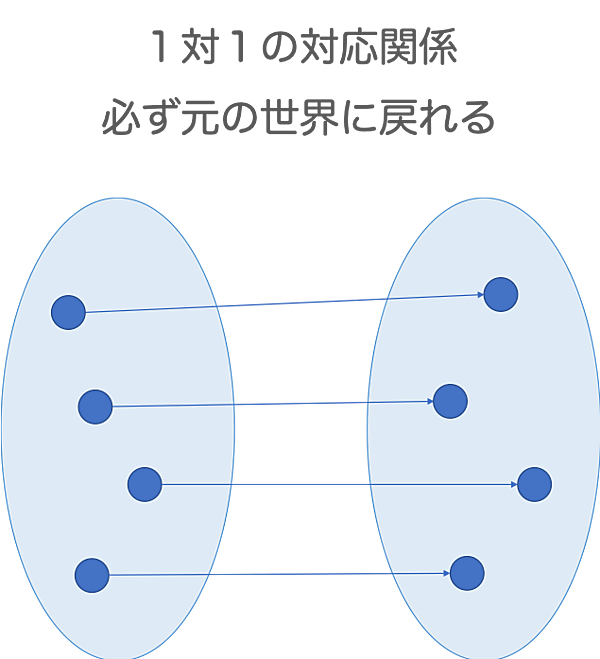
「逆行列が存在する」とは、「写った後の世界のどこからでも元の世界に戻って来ることができる」ということと同義です。もう少し数学的に言うと「写る前の世界を集合$X$、写った後の世界を集合$Y$としたとき、$X$の要素と$Y$の要素の間に1対1の対応関係がある」ということになります。もっと数学的に言えば「$X$と$Y$の間に全単射$f$が存在する」ということです。表現の仕方は色々ですが、大事なポイントは写った後の世界のどこからでも戻れるということです。

この考え方が理解できれば、逆行列が正方行列にしか存在しないことが分かります。例えば、次のような行列$A$について考えてみましょう。

$$A = \begin{pmatrix} 0 & 1 & 2 \\ 1 & 2 & 3 \end{pmatrix}$$

これは3次元の点を2次元の世界に写す変換です。試しに行列$A$を用いて点 $u_1 = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$を写してみます。つまり$Au_1$を計算するということですね。

$$Au_1 = \begin{pmatrix} 0 & 1 & 2 \\ 1 & 2 & 3 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 8 \\ 14 \end{pmatrix}$$

$x$は2次元平面上の点になりました。平面の世界です。続いて $u_2 = \begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix}$ を写してみます。

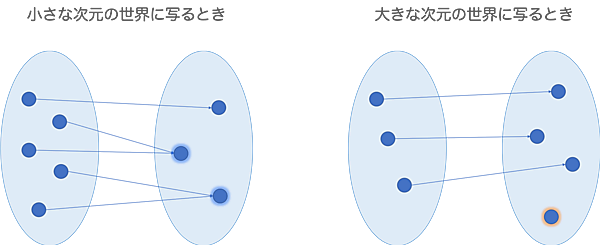
$$Au_1 = \begin{pmatrix} 0 & 1 & 2 \\ 1 & 2 & 3 \end{pmatrix} \begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix} = \begin{pmatrix} 8 \\ 14 \end{pmatrix}$$

$u_1$を写した場合と同じ結果になってしまいました。実は行列$A$を用いて $\begin{pmatrix} 8 \\ 14 \end{pmatrix}$ という点に写すことのできる3次元の点は無数にあります。これは、いざ $\begin{pmatrix} 8 \\ 14 \end{pmatrix}$ という点から戻ろうとしたとき、戻るべき場所の候補が無数にあることを意味します。非常に困った状況ですね。平面的な2次元の世界よりも立体的な3次元の世界の方が広いので、狭い世界に写ろうとするとどうしても重なる点が出てきてしまいます。残念ながら3次元の世界から2次元の世界に写動してしまうと元の世界には戻れないようです。

続いて、3次元から4次元への変換$B$を考えてみましょう。

$$B = \begin{pmatrix} 0 & 1 & 2 \\ 1 & 2 & 3 \\ 2 & 3 & 4 \\ 3 & 4 & 5 \end{pmatrix}$$

4次元の世界の方が広いので、行列$A$が引き起こしたような状況には(ある特別な状況を除いて)なりません。しかし、広いからこそ起こりうる問題があります。それは4次元の世界の一部は戻るべき3次元の点がそもそもないということです。

$$y = Bx$$

という変換を考えたときには、いかなる$y$からも$x$へ戻れなければ逆行列は存在しません。しかし、3次元の点を写して4次元の世界を全て網羅することはできないので、そもそも対応付けのできない点が出てきてしまします。4次元の世界から3次元の世界に写るのも一方通行になります。

なお、正方行列であればいつでも元の世界に戻ることができるかと言えば、そうでもありません。3次元の正方行列$C$

$$C = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 9 \end{pmatrix}$$

について考えると、

$$\begin{pmatrix} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 9 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$$ $$\begin{pmatrix} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 9 \end{pmatrix} \begin{pmatrix} 0 \\ 2 \\ -1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$$

というように、同じ点に写ってしまうことがあります。行列$C$は3次元空間への写像であることに間違いないのですが、実は全ての点がある直線上に乗ってしまいます。これを「行列の退化」といい、この現象は長方形の行列でも起こり得ます。

ところで、逆行列があれば連立方程式を解くことができる(正確にはただ1つの解を得られる)というのが第7回の内容でした。数学の目的の1つとして「方程式を解いて答えを導きたい」ということがありますから、行列式の値を持つかというのは非常に重要なポイントになります。難しいことを意識せずに行列式の値だけを見れば良いというのは非常に楽ですね。

機械学習に関連のある例を1つ挙げましょう。これまでも度々登場した二乗誤差$e$を最小にするパラメータは勾配降下法を用いても良いのですが、実は正規方程式というものを解けば一発で得られます。この方程式を解くには逆行列を求める必要があり、やはり行列式の値を確かめなければなりません。特にコンピュータを用いる場合には注意が必要です。逆行列が存在しない行列に対して逆行列を求めようとすると、エラーでプログラムが停止してしまいます(実際は行列式の概念を一般化した「擬似逆行列」というものを使うことができるため、行列式の確認をスキップすることも可能です)。

おわりに

3次元の世界を2次元に変換した後、元の3次元の世界に変換し直してくれる奇跡のシステムがこの世に1つだけ存在します。眼と脳です。眼は外界の3次元情報を網膜という2次元のスクリーンに写します。そして脳は、そのスクリーンに映った2次元の情報を元に、今まさに私たちが見ている3次元の世界を作り出します。とても不思議ですね。脳は一体何をしているのでしょうか(もちろんこれは感覚的な話でトリックがあります。全く同じ世界を再現している訳ではありません)。

ところで最近、2次元の画像からそこに映る立体を3次元的に再現するAIの開発が活発です。AIは一体何を見ているのでしょうか。機械学習どころか数学の話からも離れていきそうなので、この辺りで止めておきましょう。

さて、次回は線形代数の難所の1つである「固有値・固有ベクトル」に触れていきます。固有と言うからには何かしらのユニークさがあるわけです。そしてきっとそのユニークさが大事な特徴なのでしょうね。次回もお楽しみに。