実感しよう! スパース性が「潜む」データ

信号に潜むスパースを実感しよう!

「スパース」(sparse)とは、元々「まばらな」「希薄な」 という意味を持ちますが、データ分析の文脈では

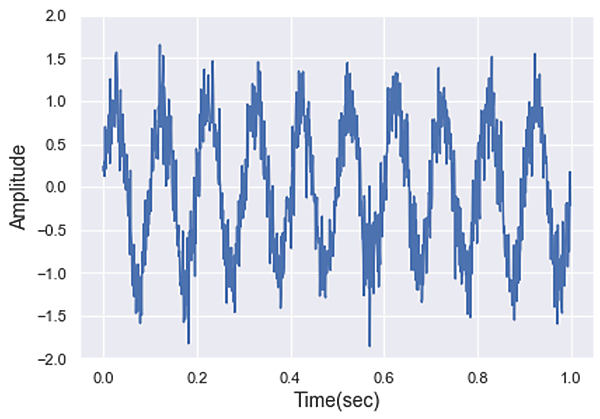
といった意味合いで使われることが多いです。少し抽象的ですね。具体例を通してスパースの気持ちを実感することが今回の目的です。まずは、下図のような信号を例にして考えてみましょう。

図1：sin波にノイズを加えた信号

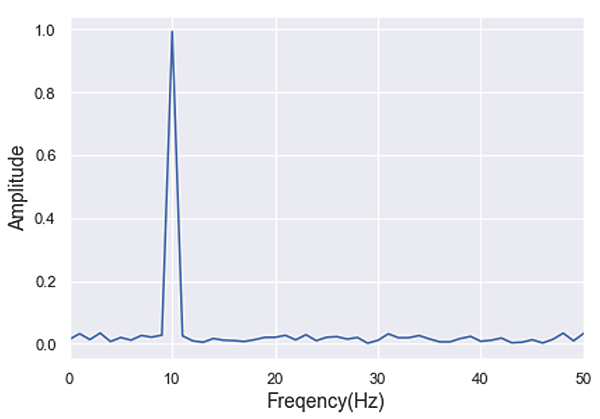
この信号は周期的な動きをするsin波にノイズが加わったものです。一見したところスパースな雰囲気はありませんね。では、この信号にフーリエ変換を施して(図2)、周波数の領域でこの信号を見てみましょう(私たちが触れ合う多くの信号は多くの異なる周波数を持つ信号の和で表現できます。フーリエ変換という技術を用いると元信号を構成する各周波数成分の強度を知ることができます)。

図2：図1の信号をフーリエ変換した結果

10Hzのところにピークが1つ立ち、それ以外の周波数成分は10Hzの振幅と比べると極端に小さく、0に近いことが分かります。この信号の本質を表す周波数成分は10Hzの波ただ1つと言って差し支えないでしょう。この信号は周波数領域においてスパースな性質を持っていると言えます。

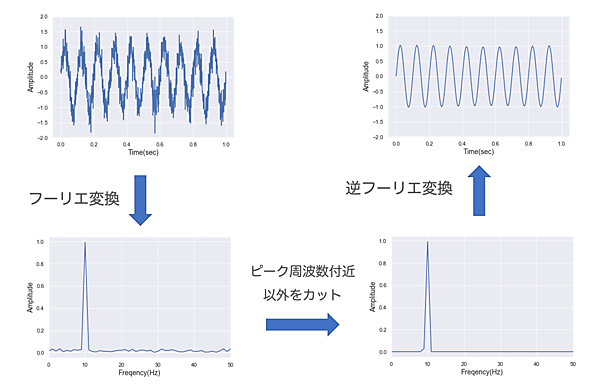
10Hzの周波数成分だけを残して逆フーリエ変換で時間領域に戻してあげれば、時間領域における信号の本質的な情報を抽出できます。実際に実行した結果が図3です。この処理は典型的なノイズ除去処理です

図3：信号からのノイズ除去

画像に潜むスパースを実感しよう!

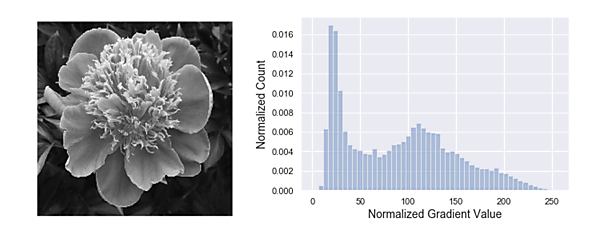
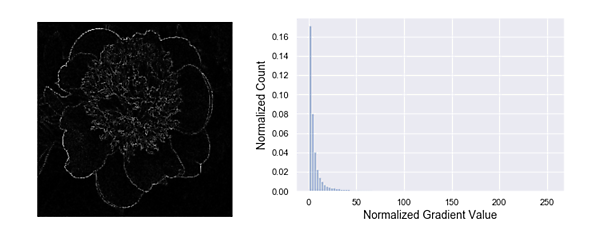
続いて、画像について考察してみます。画像とは画素値の集合なので、画像の数値データとしての側面を観察するためにはヒストグラムが良いでしょう。図4はグレースケールに変換された花の画像と、画素値のヒストグラムを表わしています。

図4：(左)グレースケール表示された花の画像 (右)画素値のヒストグラム

ヒストグラムを見ると、どの画素値もそれなりに頻度があるため、スパースな雰囲気はありませんね。この画像も見方を変えて、スパースな性質がないかを探ってみましょう。まず、画像に微分処理を行ってみます。画像に対する微分とは、つまり「画素値の変化量」を計算することです。花の画像に「ラプラシアンフィルタ」と呼ばれる微分フィルタを適用すると図5のような画像が得られました。

図5：(左)微分フィルタ適用後の花の画像 (右)微分値のヒストグラム(絶対値に変換してMax-Min正規化後に255倍している)

画像を見ると、綺麗に花の輪郭が取れていますね。輪郭とは画素値の変化が大きい領域、つまり微分の値が大きくなる領域です。輪郭以外の物体の内部の画素値は同じような値を取るため、微分の値は0に近くなります。極端なことを言ってしまえば、花という物体を形成するためには輪郭の情報しか必要ありません。微分情報という観点では、この花の画像もスパースな性質を持つと言えます。

最後に、周波数領域で花の画像を観察してみましょう。画像を二次元の信号と解釈すればフーリエ変換を適用できます。図6は先ほどの花の画像に二次元フーリエ変換を適用した例です。画像中央が明るく光り、中央から離れるにつれて暗くなっています。これは低周波成分が多く含まれ、高周波成分はあまり含まれていないことを意味しています。

図6：(左)グレースケール表示された花の画像 (右)二次元フーリエ変換の結果

画像における周波数は「1ピクセルの移動でどれほど画素値が変化するか」を表しています。1ピクセルの移動で大きく画素値が変化すると「高周波である」ということです。横軸が水平方向の周波数成分の強さ、縦軸が垂直方向周波数成分の強さを表します。

この花の画像も周波数領域においてスパースな性質を持っていると言えます。最後にこのスパース性を利用して、花の画像からノイズ除去をしてみましょう(図7)。ノイズは通常、画素値に極端な変化をもたらす高周波な成分です。花の画像の本質が低周波成分であるならば、高周波なノイズが加わっても低周波成分の抽出により綺麗な花の画像に戻るはずです。

図7：花の画像からのノイズ除去

図7中央上部の画像は、オリジナルの花の画像にノイズを加えたものです。細部が視認できないほどの比較的強いノイズを加えています。一方、右側上部の画像はノイズ除去処理を施したものです。左側上部のオリジナル画像と比べるとややぼやけていますが、花の作りの細部が視認できる程度にはノイズ除去成功していることが確認できますね!

スパース性をモデル化する!

今回は、一次元の信号と二次元の画像からスパース性を見出し、そのスパース性を活用して信号のノイズ除去を試みました。この話は一次元信号や画像に限ったことではありません。ノイズが付与された何らかの観測データがあったときに、その観測データをスパースな表現にうまく変換すれば、元の信号に復元できる可能性を秘めています。加えて、ゼロに近い成分をうまく特定できれば、少ないデータ数で原信号を復元できるかもしれません(ちょうど図2や図7で一部分の周波数領域の情報だけを用いて、元の信号とほとんど同じような信号を復元できたように!)。

このように「スパース性が存在する(0が含まれている/重要な特徴は局在する)」ということを考慮して(モデル化して)、信号復元を含め各種データ分析を行う取り組みを「スパースモデリング」と呼んでいます。

いよいよ本連載も最終回となります。次回は、このスパースモデリングについて解説します。お楽しみに!