はじめに
第4回では、線形代数、特に行列とベクトルを用いて出力層に繋がる全結合の重みの更新を統一的に表しました。機械学習・深層学習の文脈においては、込み入った数式をシンプルに記述する「表記としての線形代数」が非常に重要です。また、コンピュータ上の実装を考えるときにも線形代数のアイデアは大活躍します。
例えば、入力や重みはプログラミングにおけるarray(用いるプログラミング言語によって名称は変わります)というデータ構造でまとめることが多く、これはベクトル・行列に非常に近いアイデアです。これからも学習を続け、ぜひ線形代数に慣れ親しんでいってください。
さて、ここからが今回のメイントピック。前回までは「入力値の前向き伝播」を行い、その後「誤差の更新」を考えました。今回は「誤差の更新項を具体的にどうやって計算するのか」ということに焦点を当てていきます。つまり「勾配降下法における$\frac{ ∂E }{ ∂W }$はどうやって求めるのか」ということです。そこで登場するのが「バックプロパゲーション」と呼ばれるアルゴリズム。このアルゴリズムと勾配降下法を組み合わせることで、ニューラルネットワークの重みの更新をばっちり行うことができます。
ニューラルネットの火付け役 - バックプロパゲーション
バックプロパゲーション(誤差逆伝播)は、英語でBack Propagationと書きます。すなわち、後ろ向きに(Back)、伝える(Propagation)ということ。一体何を伝えるのかを簡単に言うと、ニューラルネットワークの文脈では「偏微分の値を出力から逆方向に各層内のニューロン達に伝える」のです。こんなことを考える背景には「勾配降下法」があります。
t 回目の全ての重みの更新式(勾配降下法)
$w^{ (t+1) } ← w^{ (t) } - ρ \frac{ ∂E }{ ∂W } (ρ > 0 )$
勾配降下法では、ネットワーク内の全ての重みについて$\frac{ ∂E }{ ∂W }$を計算しなければなりません。しかし、よく考えてみると出力層から遠く離れた中間層の結合の重みで誤差関数を偏微分するというのは、少しイメージができませんね。そこでバックプロパゲーションでは、$\frac{ ∂E }{ ∂W }$を一発で計算するのではなく、出力層のニューロンから目的のニューロンまでの経路で得られる様々な偏微分の値を用いて$\frac{ ∂E }{ ∂W }$の計算を可能にします。より具体的には「連鎖律の原理」という非常に強力な微分の法則を用います。
バックプロパゲーションのカギ - 連鎖律の原理
バックプロパゲーションと呼ばれるアルゴリズムでは、連鎖律の原理が非常に重要な役割を担います。まずは簡単な具体例から、連鎖律の原理を理解しましょう。
$$y(w_1, w_2) = (w_1x_1 + w_2x_2)^2$$
という$w_1, w_2$の関数を考えます($x_1, x_2$は定数)。この関数の見方を変えてみます。$y(w_1, w_2)$を2つの関数の合成と見なすのです。例えば、今回の場合は、
$$y = s^2$$
$$s = w_1x_1 + w_2x_2$$
という2つの関数の合成と見なします。さて、この状況で$\frac{ ∂y }{ ∂w_1 }$を考えてみましょう。$y$は一見すると$s$の関数であり、$w_1$で偏微分できそうにありません。しかし、$s$自体は$w_1$の関数となっています。このとき、偏微分を以下のように分解できるのです。
$$\frac{ ∂y }{ ∂w_1 } = \frac{ ∂y }{ ∂s } \frac{ ∂s }{ ∂w_1 }$$
これが連鎖律の原理です。$y(w_1,w_2)$を2つの関数に分解できたように、$\frac{ ∂y }{ ∂w_1 }$も2つの偏微分に分解して掛け合わせれば良いのです。
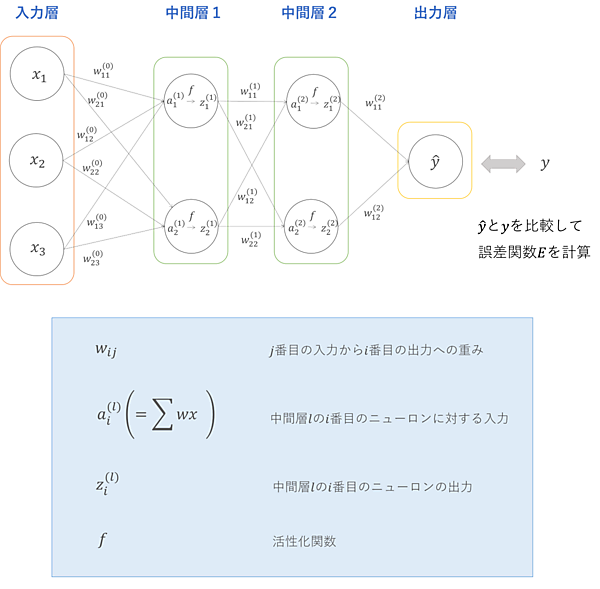
この連鎖律の原理がバックプロパゲーションのカギです。つまり「偏微分の数珠つなぎのアイデアを用いて、あらゆる重みに対する誤差関数$E$の偏微分の値を求めよう!」ということをしていくのです。そうすれば勾配降下法を用いて重みの値を更新できます。このアイデアを、2つの中間層を持った下図のような深層ニューラルネットワークを用いて具体的に考えていきましょう。
今回は中間層1の1つ目のニューロンから中間層2の1つ目のニューロンへの重み$w_{ 11 }^{ (1) }$の更新ついて考えます。つまり$\frac{ ∂E }{ ∂w_{ 11 }^{ (1) } }$を求めることが目標です。まず、誤差関数$E$は$\hat{ y }$の関数となるので、
$$\frac{ ∂E }{ ∂w_{ 11 }^{ (1) } } = \frac{ ∂E }{ ∂\hat{ y }} \frac{ ∂y }{ ∂w_{ 11 }^{ (1) } }$$
と考えることができます。次は$\frac{ ∂\hat{ y } }{ ∂w_{ 11 }^{ (1) } }$が問題です。$\hat{ y }$を計算するときには中間層2にある2つのニューロンからの出力が必要になるので、出力それぞれについて連鎖律を考えると、
$$\frac{ ∂\hat{ y } }{ ∂w_{ 11 }^{ (1) } } = \frac{ ∂\hat{ y } }{ ∂z_{ 1 }^{ (2) } } \frac{ ∂z_{ 1 }^{ (2) } }{ ∂w_{ 11 }^{ (1) } } + \frac{ ∂\hat{ y } }{ ∂z_{ 2 }^{ (2) } } \frac{ ∂z_{ 2 }^{ (2) } }{ ∂w_{ 11 }^{ (1) } }$$
となります。
続いて、$z_{ 1 }^{ (2) }$と$z_{ 2 }^{ (2) }$を$w_{ 11 }^{ (1) }$で偏微分する必要がありますが、こちらも連鎖律の原理を使えば、
$$\frac{ ∂z_{ 1 }^{ (2) } }{ ∂w_{ 11 }^{ (1) } } = \frac{ ∂z_{ 1 }^{ (2) } }{ ∂a_{ 1 }^{ (2) } } \frac{ ∂a_{ 1 }^{ (2) } }{ ∂w_{ 11 }^{ (1) } }$$
$$\frac{ ∂z_{ 2 }^{ (2) } }{ ∂w_{ 11 }^{ (1) } } = \frac{ ∂z_{ 2 }^{ (2) } }{ ∂a_{ 2 }^{ (2) } } \frac{ ∂a_{ 2 }^{ (2) } }{ ∂w_{ 11 }^{ (1) } }$$
となります。$z_{ 1 }^{ (2) } = f \Bigl(a_{ 1 }^{ (2) } \Bigr)$ , $z_{ 2 }^{ (2) } = f \Bigl(a_{ 2 }^{ (2) } \Bigr)$なので、$\frac{ ∂z_{ 1 }^{ (2) } }{ ∂a_{ 1 }^{ (2) } }$と$\frac{ ∂z_{ 2 }^{ (2) } }{ ∂a_{ 2 }^{ (2) } }$は問題なく偏微分できそうですね。また$a_{ 1 }^{ (2) }$と$a_{ 2 }^{ (2) }$は図の通り$w_{ 11 }^{ (1) }$の関数になっているので、これも問題なく偏微分できます。これで、出力層から後ろに遡って全て偏微分できる所までたどり着きました。これがバックプロパゲーションです。結局、$\frac{ ∂E }{ ∂w_{ 11 }^{ (1) } }$の項は具体的には以下のような偏微分の数珠つなぎを計算すれば良いことになります。
$$\frac{ ∂E }{ ∂w_{ 11 }^{ (1) } } = \frac{ ∂E }{ ∂\hat{ y } } \frac{ ∂\hat{ y } }{ ∂z_{ 1 }^{ (2) } } \frac{ ∂z_{ 1 }^{ (2) } }{ ∂a_{ 1 }^{ (2) } } \frac{ ∂a_{ 1 }^{ (2) } }{ ∂w_{ 11 }^{ (1) } } + \frac{ ∂E }{ ∂\hat{ y } } \frac{ ∂\hat{ y } }{ ∂z_{ 2 }^{ (2) } } \frac{ ∂z_{ 1 }^{ (2) } }{ ∂a_{ 1 }^{ (2) } } \frac{ ∂a_{ 1 }^{ (2) } }{ ∂w_{ 11 }^{ (1) } }$$
この考え方は、どんなに層が深くなっても適用できます。ただ、手計算での導出は流石に大変なので、各種プログラミング言語のライブラリを使っ方が賢明です(pythonだと例えばPreferred Networks社のChainnerが代表的です)。
バックプロパゲーションの限界
層の数と各階層を構成するニューロンの個数を増やすことによって入出力関係の表現能力を向上させるという深層ニューラルネットワークのアイデアは非常に強力で、画像認識や音声認識など産業における応用も非常に多いと聞きます。しかしながら、この深層ニューラルネットワークが大規模になるにつれてバックプロパゲーションを用いた学習は上手くいかなくなるということが知られています。
その理由として、まず学習すべき重みが非常に多くなるため、最適な値を見つけることが難しくなることです(初期値などに依存する「局所解」と呼ばれる、最適とは言えない解しか得られないことが多々あります)。また、出力から入力へ向けて誤差を伝播する過程で勾配の値(偏微分の値)が0になってしまい、重みを更新できなくなるという致命的な問題が生じることもあります(これを勾配消失問題といいます)。これは連鎖律が勾配の積となっているため、1以下の値を掛け算していくと必然的に値が小さくなることに起因しています。アルゴリズムの性質上、これは仕方がなさそうですね。
このような問題に対応するため、活性化関数や学習手法、もしくはニューラルネットワークの構造そのものを変更したりするなど、様々な工夫が提案されています。例えば、現在画像認識の分野で爆発的な人気を誇る畳み込みニューラルネットワーク(Convolutional Neural Network; CNN)は、誤差が消失しないようにニューラルネットワークの構造を工夫した代表例です。
おわりに
今回まで、微分という勾配降下法のコアを担う数学的基盤を学び、そして線形代数という機械学習のアルゴリズムを記述するうえで欠かせないツールを学びました。そして偏微分における「連鎖律の原理」を学ぶことで、重み更新の具体的な計算手法を提供するバックプロパゲーションと呼ばれるアルゴリズムを解説しました。これで深層ニューラルネットワークの重要なところは完全に理解できたといっても過言ではありません!
次回以降は、機械学習における線形代数の役割を少し深く覗いてみましょう。機械学習において線形代数は「表記」として非常に重要な役割を担いますが、実に様々な所で使われているのが分かるかと思います。大学1年生の教養数学として採用されている線形代数ですが、「これって何に役立つのだろう」と思われた方も多いはず。少しでも線形代数の魅了が伝われば幸いです。それでは、次回もお楽しみに!