暗号解読とストリーム暗号

暗号を解読するということ

　第1回（http://thinkit.co.jp/article/810/1/）では暗号の概要について述べた。今回は特に鍵の安全性と解読について解説し、ストリーム暗号の仕組みを紹介する。

　なお、本文中の計算式において、「_」は続く文字列を下付きに添えることを、「^」は文字列を上付きに添えることを表す。例えば、k_{c}はkに対してcという文字を下付きに添えることを表し、f^{-1}はfに対して-1を上付きに添えることを表し、つまりfの-1乗を示している。

　さて、暗号の安全性にとって鍵と呼ばれるパラメータが重要であり、暗号の安全性は鍵の推定問題に帰着することは前回述べた通りである。鍵を推定することが鍵の全数探索と等価となることを理想として、暗号は設計されている。

　しかし、与えた暗号アルゴリズム（暗号化関数）において、鍵を推定することが、鍵の全数探索と等価であることを証明するのは非常に困難である。よって通常は、鍵の安全性の主張として、代表的な解読方法（鍵推定法）に対して耐性があり、かつ従来知られている、いかなる方法であっても鍵の全数探索以下の計算量では、鍵を導出できないこと示している。

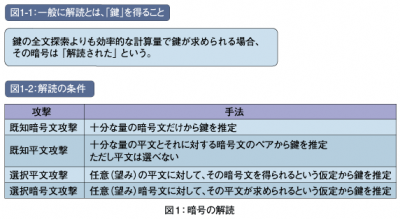
　暗号を研究する上での共通の認識として、鍵の全数探索よりも少ない計算量で、鍵を求めることができる場合、その暗号アルゴリズムに大きな欠点があるということになり、「解読された」と言う。

　しかし、現実的に鍵を導出することと、「暗号を解読すること」とは必ずしも同一ではない。

　例えば、128ビット鍵の暗号において、2^{120}の計算量で求める方法があった場合、この暗号は解読されたと言われる。しかし、実際には計算量が大きすぎて、鍵を導出することができない。ここで、基本演算、あるいは1つの鍵を確かめる演算に、パソコン1台が1ナノ秒必要であると想定すると、そのようなパソコンを1台有する個人が1日程度で鍵を導出するために必要な計算量は約2^{40}である。つまり、128ビット鍵の暗号が40ビット鍵の暗号と同じ程度の強度であるならば、1日程度で鍵を導出できるが、128ビット鍵が120ビット鍵と同じ強度になったとしても、計算量的には困難であることに変わりはない。

　本連載の主題であるWEPも提案されてまもなく、104ビット鍵のWEPであっても、鍵の全数探索よりも少ない計算量で鍵を求める方法が開発された。よって暗号としては重大な欠点を有することとなり、解読されたという認識があった。しかし、注意深く鍵を設定した一般的なWEPにおいて、実際に鍵を導出するためには、多大の計算量を含めて、さまざまな厳しい条件が必要であり，容易に鍵を導出することはできなかったのである。

ショートカットアタック

　第1回でも述べたように、鍵の全数探索となる解読方法をブルートフォースアタックと呼び、それとは異なる方法をショートカットアタックと呼ぶ。

　ブルートフォースアタックの中には「辞書攻撃」と呼ばれる暗号やパスワードの解読法が含まれる。これは暗号の鍵やパスワードに選ばれやすい意味のある語句やフレーズを、可能性の高い順に確かめていくオフライン型の攻撃である。従来、暗号解読ツール、あるいはパスワードクラッキングツールと呼ばれているものの大部分は、この辞書攻撃をベースにしている。辞書攻撃は、暗号を解読する方法ではなく、鍵の運用方法（設定方法）の脆弱（ぜいじゃく）性を突いた攻撃方法である。

　ショートカットアタックとして、有効かつ代表的な攻撃法は、「差分解読法」と「線形解読法」である。

　詳細は割愛するが、差分解読法とは、2つの平文の差が、出力となる暗号文2つの差にどのように影響するか、特に相関が存在するかを検証し、わずかな相関を元に鍵を推定する方法である。

　この差分解読法を行うためには、特定の平文とそれに対応する暗号文のペアが必要となる。任意の平文に対して、その暗号文とのペアが得られるという環境での暗号解読を「選択平文攻撃」と言う。対して、任意ではないが、十分多くの平文と、それに対する暗号文のペアが得られるという環境での暗号解読を「既知平文攻撃」と呼ぶ。後者は盗聴ができる環境であれば、十分現実的な解読法となっているが、前者は解読者が特定する平文を暗号化させる必要があり、やや現実的な環境から離れる。

　線形解読法とは、現実的な解読法となる既知平文攻撃である。線形解読法では、暗号化関数を線形近似する式を導き、その線形近似式から鍵を推定する方法である。米国商務省標準暗号であったDESは、線形解読法によって、初めて鍵の全数探索よりも小さな計算量で鍵を推定することが可能となった。現在の暗号は、これらの差分解読法と線形解読法に耐性があるように設計されている。