はじめに
本記事では、物理エンジン「Tiny2D.js」のコードを見ながら、どのような構造になっているのかを見てゆきます。まずは、こちらからTiny2D.jsのコードをダウンロードしてください(JSGameRe_Physics.zip)。本記事とコードを見比べながら読み進めることで、より理解が進むでしょう。Visual Studio Codeをインストールしていない人は、拡張子をhtmlやtxtに変換することでコードを見ることができます。
物理エンジン「Tiny2D.js」のコード詳細解説
それでは、さっそくTiny2D.jsのコードを見てみましょう。たった250行程度しかありません。順番に解説していきます。定数の定義
まず、先頭でさまざまな定数を定義しています。
定数の定義
"use strict";
let BodyStatic = 1;
let BodyDynamic = 2;
let ShapeCircle = 3;
let ShapeRectangle = 4;
let ShapeLine = 5;
ベクトル用クラスの定義
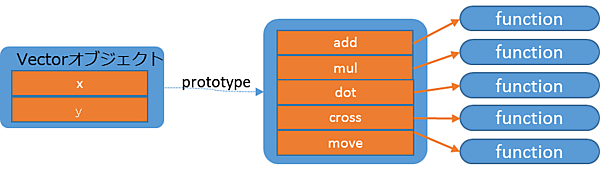
ベクトル用のクラスの定義は以下の通りです。Vecはプロパティxとyを持ち、プロトタイプにadd、mul、dot、cross、moveという5つのメソッドを定義しています。
ベクトル用クラスの定義
function Vec(x, y) {
this.x = x;
this.y = y;
}
Vec.prototype.add = function (v) { // 加算
return new Vec(this.x + v.x, this.y + v.y);
}
Vec.prototype.mul = function (x, y) { // 掛算
let r = y || x;
return new Vec(this.x * x, this.y * r);
}
Vec.prototype.dot = function (v) { // 内積
return this.x * v.x + this.y * v.y;
}
Vec.prototype.cross = function (v) { // 外積
return this.x * v.y - v.x * this.y;
}
Vec.prototype.move = function (dx, dy) {// 自分を移動
this.x += dx;
this.y += dy;
}
矩形/線オブジェクトの定義
矩形オブジェクトの定義は以下の通りです。コンストラクタの引数は左上座標(x, y)と大きさ(width, height)です。
矩形/線オブジェクトの定義
// 矩形オブジェクト
function RectangleEntity(x, y, width, height) {
this.shape = ShapeRectangle;
this.type = BodyStatic;
this.x = x;
this.y = y;
this.w = width;
this.h = height;
this.deceleration = 1.0;
this.isHit = function (i, j) {
return (this.x <= i && i <= this.x + this.w &&
this.y <= j && j <= this.y + this.h)
}
}
shapeは形状、typeは移動するか(BodyDynamic)、固定するか(BodyStatic)を指定します。矩形はエンジンによる移動対象ではないのでBodyStaticとしています。また、座標(x, y)とサイズ(w, h)というプロパティも設定しています。decelerationは減速度合です。矩形は動かさないので1を指定しています。isHitは衝突判定用のメソッドで、(i, j)が矩形の中にあるときにtrueを返します。
線オブジェクトの定義は以下の通りです。コンストラクタの引数は始点(x0, y0)、終点(x1, y1)、と反発係数restitutionです。
線オブジェクトの定義
// 線オブジェクト
function LineEntity(x0, y0, x1, y1, restitution) {
this.shape = ShapeLine;
this.type = BodyStatic;
this.x = (x0 + x1) / 2;
this.y = (y0 + y1) / 2;
this.x0 = x0;
this.y0 = y0;
this.x1 = x1;
this.y1 = y1;
this.restitution = restitution || 0.9;
this.vec = new Vec(x1 - x0, y1 - y0);
let length = Math.sqrt(Math.pow(this.vec.x, 2) + Math.pow(this.vec.y, 2));
this.norm = new Vec(y0 - y1, x1 - x0).mul(1 / length);
}
まず、shapeにShapeLineを、typeにBodyStaticを指定しています。プロパティ(x, y)は線分の中点です。また始点・終点もそれぞれプロパティとして保存します。反発係数restitutionは引数で指定された場合はその値を、省略された場合は0.9を使用します。vecは線分ベクトルで、normはその法線方向のベクトルを正規化したものです。xとyを入れ替えて、vecを長さlengthで割ること(=1 / lengthを掛ける)で求めています。
円オブジェクトの定義
円オブジェクトは長いので、分割しながら見てゆきます。まずは定義部分です。
円オブジェクトの定義
// 円オブジェクト
function CircleEntity(x, y, radius, type, restitution, deceleration) {
this.shape = ShapeCircle;
this.type = type || BodyDynamic;
this.x = x;
this.y = y;
this.radius = radius;
this.restitution = restitution || 0.9;
this.deceleration = deceleration || 1.0;
this.accel = new Vec(0, 0);
this.velocity = new Vec(0, 0);
コンストラクタの引数(x, y)は円の中心座標、radiusは半径、typeは移動する円か固定する円かの指定、restitutionは反発係数、decelerationは減速度合です。それぞれの値をプロパティとして設定します。accelは加速度ベクトル、velocityは速度ベクトルです。
円の移動
this.move = function (dx, dy) { // 円を移動
this.x += dx;
this.y += dy;
}
this.isHit = function (x, y) {
let d2 = Math.pow(x - this.x, 2) + Math.pow(y - this.y, 2);
return d2 < Math.pow(this.radius, 2);
}
moveは円を移動するメソッド、isHitは座標が円に含まれるかを判定するメソッドです。「JavaScriptで簡易物理エンジンを実装する」(https://thinkit.co.jp/article/8466)の“円と円の衝突判定”で解説したように、三平方の定理を使っています。
collidedWithRectメソッドは円(自分)と矩形(引数)の衝突処理を行います。
円と矩形の衝突処理
this.collidedWithRect = function (r) { // 円と矩形の衝突
// 矩形の4辺上で最も円に近い座標(nx, ny)を求める
let nx = Math.max(r.x, Math.min(this.x, r.x + r.w));
let ny = Math.max(r.y, Math.min(this.y, r.y + r.h));
if (!this.isHit(nx, ny)) { // 衝突なし→リターン
return;
}
if (this.onhit) { // 衝突時のコールバック
this.onhit(this, r);
}
let d2 = Math.pow(nx - this.x, 2) + Math.pow(ny - this.y, 2);
let overlap = Math.abs(this.radius - Math.sqrt(d2));
let mx = 0, my = 0;
if (ny == r.y) { // 上辺衝突
my = -overlap;
} else if (ny == r.y + r.h) { // 下辺衝突
my = overlap;
} else if (nx == r.x) { // 左辺衝突
mx = -overlap;
} else if (nx == r.x + r.w) { // 右辺衝突
mx = overlap;
} else { // 矩形の中
mx = -this.velocity.x;
my = -this.velocity.y;
}
this.move(mx, my);
if (mx) { // X軸方向へ反転
this.velocity = this.velocity.mul(-1 * this.restitution, 1);
}
if (my) { // Y軸方向へ反転
this.velocity = this.velocity.mul(1, -1 * this.restitution);
}
}
まず、“円と矩形の衝突判定”(https://thinkit.co.jp/article/8466)で解説した内容をそのまま実装しています。4辺と最も近い座標(nx, ny)を求め、それが円の中になければ衝突なしとしてreturnします。自分にonhitメソッドが定義されている場合、そのメソッドを呼び出します。d2は(nx, ny)と円の中心座標(x, y)の距離の二乗です。この値を使って重なっている距離overlapを求めます。
次に、衝突した場所に応じて円の進行方向を変化させます。(mx, my)は重なり部分の大きさで、0で初期化しておきます。これは、めり込んだ量を元に戻すための変数で、方向を反転するためにも利用します。上辺か下辺に衝突した場合は上下方向へ反転し、左辺か右辺に衝突した場合は左右方向へ反転します。
円の速度が早い場合に(nx, ny)が矩形の中に入る場合もありますが、その際はvelocityのxとyを反転して外に押し戻しています。本来は進入方向を鑑みて外に押し戻したほうが自然な動きになるので、興味のある方は修正してみてください。
その後、this.move(mx, my)で円の中心座標を移動して重なりを解消し、(mx, my)の値に応じてx軸もしくはy軸方向に速度を反転させています。
collidedWithLineは円と線の衝突を処理します。
円と線の衝突処理
this.collidedWithLine = function (line) { // 円と線の衝突
let v0 = new Vec(line.x0 - this.x + this.velocity.x, line.y0 - this.y + this.velocity.y);
let v1 = this.velocity;
let v2 = new Vec(line.x1 - line.x0, line.y1 - line.y0);
let cv1v2 = v1.cross(v2);
let t1 = v0.cross(v1) / cv1v2;
let t2 = v0.cross(v2) / cv1v2;
let crossed = (0 <= t1 && t1 <= 1) && (0 <= t2 && t2 <= 1);
if (crossed) {
this.move(-this.velocity.x, -this.velocity.y);
let dot0 = this.velocity.dot(line.norm); // 法線と速度の内積
let vec0 = line.norm.mul(-2 * dot0);
this.velocity = vec0.add(this.velocity);
this.velocity = this.velocity.mul(line.restitution * this.restitution);
}
}
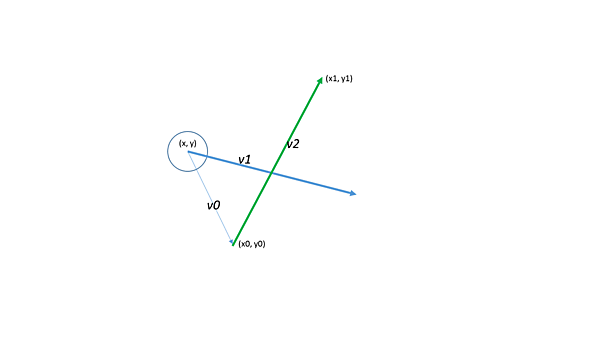
難しそうに見えるかもしれませんが、“円と線の衝突判定”で解説した内容をそのまま実装に落とし込んでいるだけです。コード中にある変数v0、v1、v2は下図の通りです。
- v0=円の中心から線分の始点へのベクトル
このコードが実行されるときには、既に速度ベクトルが加算されて移動後の場所になっています。よって速度ベクトルを引いていることに注意してください。つまり、x軸について見るとline.x0 – (this.x - this.velocity.x)という計算を行っています。これはline.x0 - this.x + this.velocity.xと同じ意味になります。 - v1=円の速度ベクトル
- v2=線分ベクトル
あとは、ベクトルの外積を求めて衝突判定を行っているだけです。衝突した場合はcrossedがtrueとなります。衝突した場合は円の速度ベクトルを変化させる必要がありますが、その計算は“動く円と静止円の衝突”で解説した内容と同じです。
this.move(-this.velocity.x, -this.velocity.y);
で衝突前の座標に戻し、法線単位ベクトルとの速度の内積を求めることで法線方向の成分を求め、その値を2倍しています。
let dot0 = this.velocity.dot(line.norm); // 法線と速度の内積
let vec0 = line.norm.mul(-2 * dot0);
あとは、もともとのベクトルにその値を加算し、最後に反発係数をかけ合わせています。これらの処理を行うことで速度ベクトルを反射しています。コード見るだけではわかりづらいかもしれませんが、“動く円と静止円の衝突”の解説と照らし合わせながら読んでゆけば理解しやすいと思います。
最後に、円と円の衝突です。この処理も“円と円の衝突判定”、“動く円と静止円の衝突”、“動く円と動く円の衝突”で解説した内容をコードに落とし込んでいるだけです。
円と円の衝突
this.collidedWithCircle = function (peer) { // 円と円の衝突
let d2 = Math.pow(peer.x - this.x, 2) + Math.pow(peer.y - this.y, 2);
if (d2 >= Math.pow(this.radius + peer.radius, 2)) {
return;
}
if (this.onhit) {
this.onhit(this, peer);
}
if (peer.onhit) {
peer.onhit(peer, this);
}
自分の円はthis、相手の円はpeerという変数で管理しています。2つの円の中心距離を求め、その値が2つの円の半径の合計よりも大きい場合は衝突していないのでreturnで戻ります。衝突した場合は自分と相手のonhitプロパティを見て、定義されている場合はそのメソッドを呼び出します。
distanceは2つの円の中心の距離を格納する変数です。
let distance = Math.sqrt(d2) || 0.01;
この行には想い入れがあるので、少し詳しく解説します。最初は以下のように実装していました。
let distance = Math.sqrt(d2);
実は、多少複雑なゲームを作ったときに、円オブジェクトがすべて画面から消えてしまうというバグに数日間悩まされました。再現性が低く、決まった再現方法はありませんでした。結局、console.logで情報を出力させつつ、辛抱強く再現をさせることでその原因が明らかにすることができました。その原因がこの行だったのです。
少し後に、以下の行があります。
let aNormUnit = v.mul(1 / distance); // 法線単位ベクトル1
もし2つの円がまったく同じ座標にあったときの中心距離は0になり、distanceも0になります。そうです! 2つの円がまったく同じ座標になったときに0で除算が行われていたのです。JavaScriptでは0で割ると結果はNaN(Not a Number)になってしまいます。一旦NaNになると、足し算をしても掛け算をしても結果はNaNとなり、円の座標が不正なため描画されなくなってしまったのです。よって、距離が0のときは0.01という小さな値を使用することでこの状況に対処しました。
overlapは重なりの距離です。vは2つの円の中心を結ぶベクトルで、これを円の中心間の距離distanceで割ることで法線ベクトルaNormUnitを求めています。bNormUnitは逆向きの法線ベクトルです。aNormUnitを-1倍することで求めています。
法線単位ベクトルを求める
let distance = Math.sqrt(d2) || 0.01;
let overlap = this.radius + peer.radius - distance;
let v = new Vec(this.x - peer.x, this.y - peer.y);
let aNormUnit = v.mul(1 / distance); // 法線単位ベクトル1
let bNormUnit = aNormUnit.mul(-1); // 法線単位ベクトル2
if (this.type == BodyDynamic && peer.type == BodyStatic) {
this.move(aNormUnit.x * overlap, aNormUnit.y * overlap);
let dot0 = this.velocity.dot(aNormUnit); // 法線と速度の内積
let vec0 = aNormUnit.mul(-2 * dot0);
this.velocity = vec0.add(this.velocity);
this.velocity = this.velocity.mul(this.restitution);
}
else if (peer.type == BodyDynamic && this.type == BodyStatic) {
peer.move(bNormUnit.x * overlap, bNormUnit.y * overlap);
let dot1 = peer.velocity.dot(bNormUnit); // 法線と速度の内積
let vec1 = bNormUnit.mul(-2 * dot1);
peer.velocity = vec1.add(peer.velocity);
peer.velocity = peer.velocity.mul(peer.restitution);
}
else {
this.move(aNormUnit.x * overlap / 2, aNormUnit.y * overlap / 2);
peer.move(bNormUnit.x * overlap / 2, bNormUnit.y * overlap / 2);
let aTangUnit = new Vec(aNormUnit.y * -1, aNormUnit.x); // 接線ベクトル1
let bTangUnit = new Vec(bNormUnit.y * -1, bNormUnit.x); // 接線ベクトル2
let aNorm = aNormUnit.mul(aNormUnit.dot(this.velocity)); // aベクトル法線成分
let aTang = aTangUnit.mul(aTangUnit.dot(this.velocity)); // aベクトル接線成分
let bNorm = bNormUnit.mul(bNormUnit.dot(peer.velocity)); // bベクトル法線成分
let bTang = bTangUnit.mul(bTangUnit.dot(peer.velocity)); // bベクトル接線成分
this.velocity = new Vec(bNorm.x + aTang.x, bNorm.y + aTang.y);
peer.velocity = new Vec(aNorm.x + bTang.x, aNorm.y + bTang.y);
}
あとは、if文で3つの場合に応じて処理を切り分けています。
- this.type == BodyDynamic && peer.type == BodyStatic
自分が動く円で相手が固定円の場合 - peer.type == BodyDynamic && this.type == BodyStatic
自分が固定円で相手が動く円の場合 - それ以外
片方が固定円の場合は、円と線の衝突と同じ処理を行っています。moveメソッドを使って重なった量を移動し、2つの物体が重なっている状態を解消します。そして法線ベクトルとの内積を求めて2倍し、それに自分自身のベクトルを足すことで反射後のベクトルを求めています。
“それ以外”の場合は、“動く円と動く円の衝突”で解説した内容をコードに落とし込んでいます。それぞれ円にmoveメソッドを使って重なった量の半分を移動し、2つの物体が重なっている状態を解消します。法線ベクトルのxとyを入れ替えて接線ベクトルを求めます。それぞれの円の法線と接線ベクトルが求められたので、自分の速度ベクトルとの内積から法線方向、接線方向の成分を求めます。それらを適切に加算することで反射後の速度を求めています。
Engineオブジェクトの定義
最後は、物理エンジンの全体を管理するEngineオブジェクトです。まずはコンストラクタと初期化部分からです。
Engineオブジェクトの定義
function Engine(x, y, width, height, gravityX, gravityY) {
this.worldX = x || 0;
this.worldY = y || 0;
this.worldW = width || 1000;
this.worldH = height || 1000;
this.gravity = new Vec(gravityX, gravityY);
this.entities = [];
this.setGravity = function (x, y) {
this.gravity.x = x;
this.gravity.y = y;
}
物理世界の左上座標を(x, y)、そのサイズを(width, height)、重力をgravityXとgravityYで指定します。コンストラクタでは、これらの値をプロパティに格納します。entitiesは円、矩形、線といった物理エンジンの世界のオブジェクトを保持する配列です。ゲームの途中で重力の向きを変えたくなるかもしれないと思ったので、メソッドsetGravityを用意しました。
stepは物理世界の時計を少しだけ進めるメソッドです。物理エンジンの中心的役割をします。これも少し長いので、分割して解説します。
stepメソッド
this.step = function (elapsed) {
let gravity = this.gravity.mul(elapsed, elapsed);
let entities = this.entities;
// entityを移動
entities.forEach(function (e) {
if (e.type == BodyDynamic) {
let accel = e.accel.mul(elapsed, elapsed);
e.velocity = e.velocity.add(gravity);
e.velocity = e.velocity.add(accel);
e.velocity = e.velocity.mul(e.deceleration);
e.move(e.velocity.x, e.velocity.y);
}
});
まず、重力に経過時間を掛けて、その時間分の速度gravityを求めています。次に配列の中で(e.type == BodyDynamic)を満たすオブジェクトに対して速度gravity、加速度accelによる変化分を加算し、減速度合いを掛け合わせています。その結果求められたvelocity分をmoveメソッドで移動させています。つまり移動対象となるオブジェクトの速度を更新し、その値に応じて移動させているのです。これで物理世界内にあるオブジェクトが移動します。
実は、本来であれば速度(velocity)に時間(elapsed)を掛けて移動距離を求め、その距離をmoveメソッドに引き渡すべきでした。現在の実装では単に速度を渡しているだけなので単位時間当たりの移動距離となっています。サンプルゲームレベルでは特に問題にならなかったので割り切ってしまいました。興味のある方は修正してみてください。
しかし、移動させただけでは不十分です。衝突を判定して、衝突した場合には速度ベクトルを反射させる必要があります。その処理内容は以下の通りです。
衝突判定と衝突処理
// 範囲外のオブジェクトを削除
this.entities = entities.filter(function (e) {
return this.worldX <= e.x && e.x <= this.worldX + this.worldW &&
this.worldY <= e.y && e.y <= this.worldY + this.worldH;
}, this);
// 衝突判定 & 衝突処理
for (let i = 0 ; i < entities.length - 1 ; i++) {
for (let j = i + 1; j < entities.length ; j++) {
let e0 = entities[i], e1 = entities[j];
if (e0.type == BodyStatic && e1.type == BodyStatic) {
continue;
}
if (e0.shape == ShapeCircle && e1.shape == ShapeCircle) {
e0.collidedWithCircle(e1);
} else if (e0.shape == ShapeCircle && e1.shape == ShapeLine) {
e0.collidedWithLine(e1);
} else if (e0.shape == ShapeLine && e1.shape == ShapeCircle) {
e1.collidedWithLine(e0);
} else if (e0.shape == ShapeCircle && e1.shape == ShapeRectangle) {
e0.collidedWithRect(e1);
} else if (e0.shape == ShapeRectangle && e1.shape == ShapeCircle) {
e1.collidedWithRect(e0);
}
}
}
まず、物理世界の外に飛び出してしまったオブジェクトを削除します。世界の外にあるオブジェクトについて計算しても無駄だからです。Array.filterを使って物理世界の中にあるオブジェクトのみを抽出しています。
次に、衝突判定です。for文の内容がいつもの単純な2重ループと異なることに注意してください。例えば、オブジェクト1とオブジェクト2の衝突判定を行ったら、オブジェクト2とオブジェクト1の衝突判定を行う必要はありません。また、自分と自分の衝突判定を行うのもナンセンスです。このような状況を避けるためにforの繰り返し範囲を調整しています。あとはオブジェクトをe0とe1として取り出し、それぞれのタイプ、形状に応じて適切なメソッドを呼び出しています。例えば、双方がBodyStaticのときはお互いに固定されているので何も処理をする必要がありません。お互いが円のときはcollidedWithCircle()を、円と線の時はcollidedWithLine()を、円と矩形のときはcollidedWithRect()をといった具合です。それぞれのメソッドについては既に解説した通りです。
以上で物理エンジンのコードに関する詳細解説は終わりです。世間一般で広く利用されている他の物理エンジンとは比べようもないほどシンプルで最低限の機能しかありませんが、入門用のきっかけとなることを目的とした題材です。まずは、このエンジンを活用したアプリを作ってみてください。そのうち機能が足りないことに不満を覚えることでしょう。そうしたら、次の段階として物理エンジンそのものに機能を追加したり、パフォーマンスを改善したり、どんどん作り変えてより良いものにしてみてください。その過程で色々なスキルを身につけることができるはずです。
物理エンジンの動作を確認してみよう
本記事の締めくくりとして、物理エンジンを使用したデモを紹介します。説明だけではなかなか理解しにくいと思いますが、実際の動きを見ることで理解が深まると思います。
デモ(demo.html)
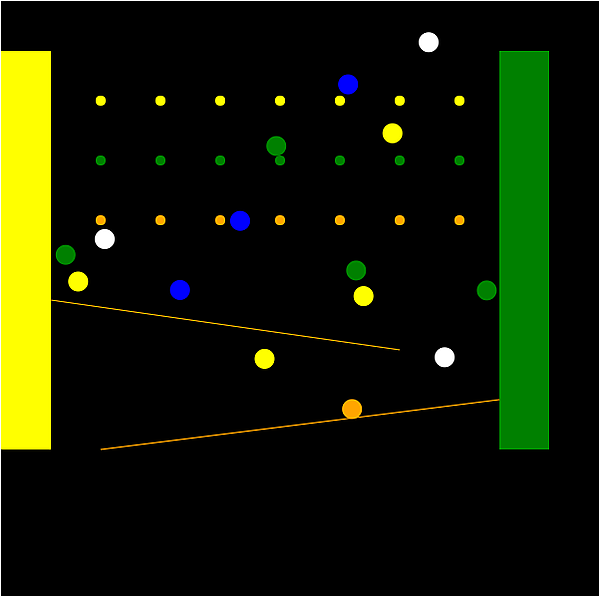
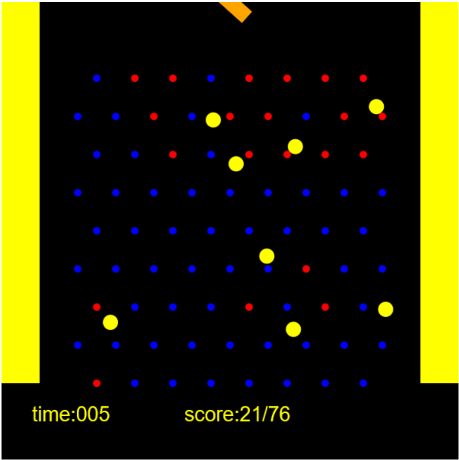
矩形、線、円(固定)、円(移動)といったオブジェクトを画面上に配置しただけのサンプルです。シンプルなページですが、それなりに面白い動きをします。
デモのサンプルは、本記事の冒頭でダウンロードしたファイルに含まれています。まずは、デモを実行して動きを確認してみましょう。
物理エンジンはいろいろなページから参照するので、別ファイル(サンプルファイル「Tiny2D.js」)に保存しました。外部のJavaScriptファイルを取り込む場合は以下のようにscript要素を使用します。
<script src="Tiny2D.js"></script>
それでは、サンプルコードを見てゆきましょう。Tiny2d.jsと同様に、コード(demo.html)を見ながら解説を読み進めてください。
広域変数は、engine(物理エンジンオブジェクト)、ctx(グラフィックコンテキスト)、colors(色の配列)の3つだけです。関数rand(v)は整数の乱数を返します。
init()
init()から実行が開始されます。物理世界を作成してオブジェクトを配置しています。
init()
function init() {
let r;
engine = new Engine(0, 0, 600, 800, 0, 9.8); ←(A)
r = new RectangleEntity(500, 50, 50, 400); // 矩形を作成しエンジンに追加
r.color = "green";
engine.entities.push(r); ←(B)
r = new RectangleEntity(0, 50, 50, 400);
r.color = "yellow";
engine.entities.push(r);
r = new LineEntity(50, 300, 400, 350); // 線分を作成しエンジンに追加
r.color = "orange";
engine.entities.push(r);
r = new LineEntity(500, 400, 100, 450);
r.color = "orange";
engine.entities.push(r);
// 7 x 3 = 21 個の円(固定)を作成
for (let i = 0; i < 7; i++) {
for (let j = 0; j < 3; j++) {
r = new CircleEntity(i * 60 + 100, j * 60 + 100, 5, BodyStatic);
r.color = colors[j];
engine.entities.push(r);
}
}
// 20 個の円(移動)を作成
for (let i = 0; i < 20; i++) {
r = new CircleEntity(rand(400) + 50, rand(200), 10, BodyDynamic);
r.color = colors[rand(5)];
r.velocity.x = rand(10) - 5;
r.velocity.y = rand(10) - 5;
engine.entities.push(r);
}
ctx = document.getElementById("canvas").getContext("2d");
setInterval(tick, 50);
}
物理世界はEngineオブジェクトとして実装されており、以下の命令で作成します(A)。
engine = new Engine(0, 0, 600, 800, 0, 9.8);
Engineオブジェクトのコンストラクタの引数は、世界のx座標、y座標、幅、高さ、x方向の重力、y方向の重力です。ここでは、左上座標(0,0)、幅600、高800で下方向に重力がある世界を作っています。
Tiny2Dでサポートしている物理オブジェクトは、以下の3種類です。
- RectangleEntity(x, y, width, height)
(x, y)を左上座標とする幅width、高さheightの矩形を作成します。 - CircleEntity(x, y, radius, type, restitution, deceleration)
(x, y)を中心座標とする半径radiusの円を作成します。typeはBodyStatic(円が固定されている)か、BodyDynamic(動的に動くか)を指定します。デフォルトはBodyDynamicです。restitutionは反発係数、decelerationは減速度合いとなります。restitution, decelerationは省略可能です。 - LineEntity(x0, y0, x1, y1, restitution)
(x0, y0)から(x1, y1) への線を引きます。restitutionは反発係数です。restitutionは省略可能です。
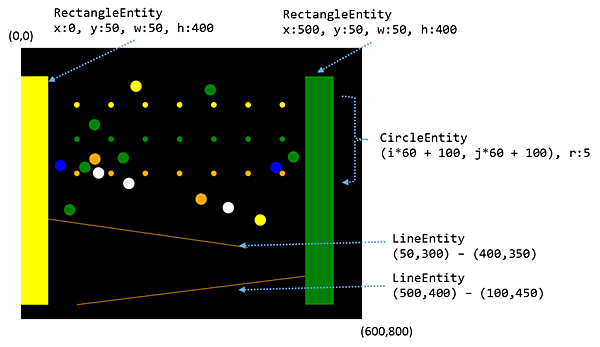
矩形、円、線と作成していますが、それぞれのオブジェクトのコンストラクタを呼び出してオブジェクトを作成しているだけです。特に難しいところはないと思います。作成しているオブジェクトの様子を下図に示します。
作成したオブジェクトはengine.entities.push(r)で物理世界に追加します(B)。あとはengine.step()で物理世界の時計を進めれば、物理世界のオブジェクトが動き始めます。その座標を取得して描画すれば、あたかも物が動いているように見えるというわけです。
ちなみに、円オブジェクトは動かすことができますが、その初速度を以下のように設定しています。
r.velocity.x = rand(10) - 5;
r.velocity.y = rand(10) - 5;
あとは最後にグラフィックコンテキストを取得し、setIntervalでメインループを開始しています。
JavaScriptではオブジェクトにプロパティを追加することができます。RectangleEntityやCircleEntityといった物理世界のオブジェクトも例外ではありません。今回は描画用にcolorプロパティを追加しています。
tick()
tick()では、エンジンの時間を0.01進め、再描画を行うという処理を行っています。
init()
function tick() {
engine.step(0.01);
repaint();
}
repaint()
repaint()では再描画を行います。
repaint()
function repaint() {
ctx.fillStyle = "black"; ←(A)
ctx.fillRect(0, 0, 600, 600);
// 物理世界のモノを描画
engine.entities.forEach((e) => {
ctx.fillStyle = e.color; ←(C)
ctx.strokeStyle = e.color;
switch (e.shape) { ←(D)
case ShapeRectangle: // 矩形の場合
ctx.fillRect(e.x, e.y, e.w, e.h);
break;
case ShapeCircle: // 円の場合
ctx.beginPath();
ctx.arc(e.x, e.y, e.radius, 0, Math.PI * 2);
ctx.closePath();
ctx.fill();
break;
case ShapeLine: // 線分の場合
ctx.beginPath();
ctx.moveTo(e.x0, e.y0);
ctx.lineTo(e.x1, e.y1);
ctx.stroke();
break;
}
}
まずAで画面全体を黒で塗りつぶしてクリアします。物理世界にあるオブジェクトは物理エンジンのentitiesプロパティ(配列)に格納されているので、Bのfor文で要素を順番に取り出します。
CでコンテキストのfillStyle(塗りつぶし色)とstrokeStyle(描画色)をその要素のcolorプロパティで設定し、Dのswitch文を使って形状に応じた処理を呼び出しています。ShapeRectangle(矩形)のときはfillRectを使って矩形を描画し、ShapeCircle(円)のときはarcを使って円を描画し、ShapeLine(線)のときはmoveToとlineToで線を描画しています。
たったこれだけで物理オブジェクトが画面上を動き回ってくれるのです。おもしろいとおもいませんか? ところで、このデモを実行していると、円が線を飛び越えるという現象に気づいた人もいると思います。実はこれはknown issueです。動く円が何かと衝突して向きを変えるとき、その速度ベクトルを変更するとともに、重なりを解消するため重なり量を移動させています。実はその際にも本当は衝突判定をすべきなのですが、このエンジンでは衝突判定をしていないのです。よって、移動量が大きかったりする場合に、このような現象が起きてしまいます。修正も考えたのですがコード量が増えそうだったので今回は見送りました。ご了承ください。
さいごに
「ゲームで学ぶJavaScript入門 増補改訂版~ブラウザゲームづくりでHTML&CSSも身につく!」では、実際にTiny2D.jsを使用した下記のようなサンプルゲームを解説しています。
これらゲームにも興味がある方は、ぜひ本書を手に取ってみてください。
- この記事のキーワード