JavaScriptで簡易物理エンジンを実装する

はじめに

本記事は、書籍「ゲームで学ぶJavaScript入門 増補改訂版～ブラウザゲームづくりでHTML＆CSSも身につく!」用に作成した簡易2D物理エンジン「Tiny2D.js」の詳細解説です。Tiny2D.jsは角速度や質量は考慮しない、矩形と円しかサポートしないなど、物理エンジンと名乗るには僭越なほどシンプルなものですが、シンプルなだけに使い方も簡単で、修正も十分に可能です。「百聞は一見にしかず」です。まずはサンプルを実行してみて、どのような動きをするのか皆さん自身で確かめてみてください。

物理エンジンとは

「アングリーバード」や「モンスターストライク」など物理エンジンを活用したパズル系のゲームが人気です。物理エンジンとは、様々な物理法則をシミュレートし、物体の衝突や動きを計算するものです。物理エンジンを利用することで実世界のようなリアルな動きを再現できますが、リアルな動きを再現するためには摩擦、衝突、慣性、重力、運動量保存、重心、角速度…といった様々な物理法則に基づいた計算を行う必要があり、その実装は容易ではありません。そのため、多くのゲームでは既存の物理エンジンを利用しています。

代表的な物理エンジンには「Box2D」「PhysicsJS」「ThreeJS」「Unity」といったものがあります。物理エンジンを使えば複雑な物理計算を自分で行わなくても済みますが、その分習得には時間と労力がかかります。「読者により興味を持ってもらうには流行の物理エンジンを使いたい、ただ既存のライブラリを使うとそれだけで本1冊のボリュームになってしまう」と悩み、極限までシンプルな物理エンジンを作ることにしました。

物理エンジンの仕組み

一般的な物理エンジンでは、最初に仮想的な空間を用意して、その中にオブジェクトを配置します。2次元エンジンなら矩形、円、ポリゴンを、3次元のエンジンであれば立方体や球などでしょう。エンジンによっては複雑な形状を指定したり、それらを組み合わせたりすることが可能です。それぞれのオブジェクトは固定されているものと動きのあるものに大別されますが、動いているものであれば速度や加速度、回転といったパラメタを指定します。

初期化が完了したら、この仮想世界の時間を少しだけ進めてみましょう。速度が設定されているオブジェクトは新しい場所へ移動します。重力加速度が設定されている場合は、その加速度も考慮されます。移動が完了したら画面を更新します。

すると、そのうちオブジェクト同士が衝突します。衝突したらオブジェクトの向きや速度を変化させます。物理エンジンの基本的な動作はこれらの作業を繰り返すだけです。

　　時計を進めて場所を計算 → 描画 → 時計を進めて場所を計算 → 描画 →…

このように物理エンジンの原理は簡単ですが、面倒なのは移動や衝突時の計算です。以下のような処理を計算で求める必要があります。

• オブジェクトの位置計算（速度・加速度・摩擦・重力・回転等）
• 衝突判定
• 衝突時の処理（反発係数・重力・エネルギー保存則等）

これらの計算をどれだけ正確に行うか、どの程度複雑な形状（とその組み合わせ）をサポートするかといったところが物理エンジンの特徴につながってゆきます。今回のエンジンはあくまでも入門用なので円・矩形・直線しかサポートしません。またオブジェクトの回転もサポートしません。移動するのは円のみで矩形と直線は仮想空間内で固定されているものとします。かなり割り切った仕様ですが、シンプルなゲームであれば十分に利用できます。

それでは、どのように物理エンジンが実装されているかを見てゆきたいと思いますが、まず前提となる知識をおさらいしておきましょう。

ベクトルの基礎

「ベクトル」とは、向きと大きさを持った量のことです。天気予報の風の向き（東北東3m/秒）、投手の投げる球（北方向に150km/時）、落下するリンゴ（下向き1m/秒）など、これらはすべてベクトルで表現できます。ちなみに、テストの点数、体重、身長といった1つの数値だけで表される量を「スカラー」と呼びます。

衝突判定や反射角といった物理エンジンに不可欠な計算にはベクトルが必要です。ベクトルは高校数学の代数幾何で学習する内容ですが、ここでは基本的な部分だけ説明するので安心してください。筆者も30年程前に代数幾何を勉強しましたが、その時は何の役に立つのかさっぱりわかりませんでした。代数幾何はゲームを作る際に必ず役立ちます。できるだけ平易に説明しますので、代数幾何を勉強中の高校生はもちろん、将来ゲーム開発に携わりたい人、やる気のある中学生、復習したいと思う大学生・専門学校生も是非ご一読ください。

ベクトルの足し算

「ベクトルは向きと大きさを持った量」と説明しました。2次元の座標系においては、始点と終点で表現することができます。

例えば、上図には2つのベクトルが表現されていますが、ベクトルであることを明確にしたい場合、上に横矢印を描画するのが一般的です。

ベクトルの始点と終点一覧

	始点	終点	ベクトル
例1	（1,3）	（4,4）	（3,1）
例2	（3,1）	（2,3）	（-1,2）

このように、2次元の座標系におけるベクトルは「（ｘ軸方向の増分、ｙ軸方向の増分）」として表現されます。例1の場合、

• ｘ軸方向の増分 ＝ 終点ｘ座標 ー 始点ｘ座標 ＝ 4 － 1 ＝ 3
• ｙ軸方向の増分 ＝ 終点ｙ座標 ー 始点ｙ座標 ＝ 4 － 3 ＝ 1

となるので、ベクトル成分は（3,1）となります。

ベクトルの足し算は簡単です。それぞれのベクトルのx成分、ｙ成分を足し算すれば良いだけです。例えば、ベクトル（1,2）と（3,1）を加算すると以下のようになります。

　（1,2）＋（3,1）＝（4,3）
　　ｘ成分の加算 ＝ 1 ＋ 3＝ 4
　　ｙ成分の加算 ＝ 2 ＋ 1 ＝ 3

これは座標系でのベクトルの様子を見てみるとよくわかります。

ベクトルの掛算

「ベクトルの掛算」とは、x成分、y成分の両方に同じ数をかけることです。例えば、（2,1）というベクトルを2倍すると（4,2）に、0.5倍すると（1,0.5）になります。また、「正規化」とは、向きはそのままで長さを1にすることを言います。これもベクトルの掛け算で求められます。

ベクトルの内積

ベクトルの内積は“・”で表現します。計算式は以下の通りです。

　　v1・v2 = v1のx成分 × v2のx成分 ＋ v1のy成分 × v2のy成分

計算結果はベクトルではなくスカラー値（単なる数値）となります。例を見てみましょう。

上図の例では、v1・v2 = 1×3 ＋ 2×0 ＝ 3となります。

でも、この値が何を意味するのかわかりませんよね？ 証明は専門書に譲りますが、この計算結果は次の計算式で求めた値と同じになります。

　　v1・v2 = |v1| × |v2| × cosθ

ここで|v1|はベクトルv1の大きさ、|v2|はベクトルv2の大きさ、θは2つのベクトルのなす角度です。θが0°のときcosθは1になります。このとき、内積は｜v1｜×|v2|となり最大の値を取ります。一方、θが90°のときcosθは0になり、内積の値は0となります。つまり、2つのベクトルの向きが近いほうが内積は大きな値になるのです。多少乱暴ですが、「内積とは2つのベクトルがどの程度同じ方向を向いているのかを表す値」と理解しても良いでしょう。

この関係をうまく利用すると、2つのベクトルのなす角を簡単に求めることができます。先ほどの例では、v1(1,2)、v2(3,0)でした。始点をそろえると下図のようになります。

内積の計算結果は3だったので、3 ＝ |v1| × |v2| × cosθとなります。v2の大きさは3です。v1の大きさは√(1²+2² ) ＝ √5です。つまり、3 =（3×√5）× cosθとなり、この式を解くことでcosθの値が求まります。cosθが分かればθも計算できます。

物理エンジンで2つの物体が衝突して反射する状況を考えてみましょう。2つの物体の進み度合であるベクトルの内積から反射角を計算し、衝突後の向きを計算することもできそうです。しかしながら、ベクトルを使えばもっと簡単に衝突後の向きを計算することができます。詳しくは後述しますが、基本的な簡単な考え方だけをここで説明しておきます。

まず、三角関数のおさらいをしておきましょう。直角三角形の斜辺が1のとき、sinθとcosθは以下のように求められます。この三角形がv倍されたとすると、それぞれの辺の長さはv×sinθ、v×cosθとなります。

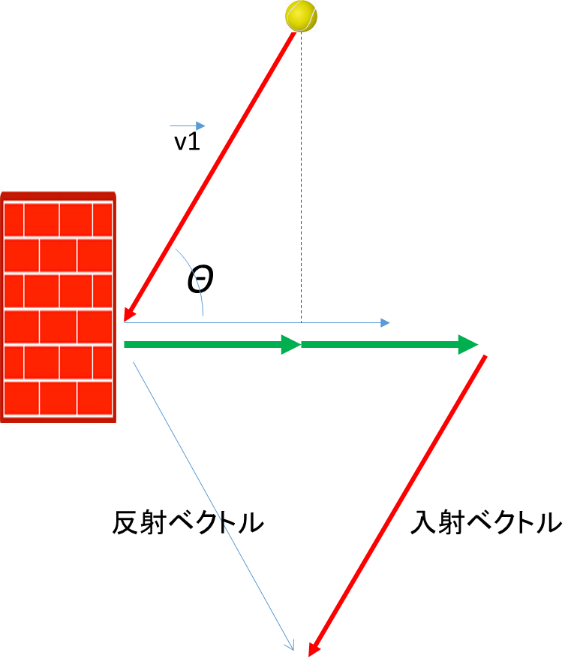
ベクトルv1で進むボールが、下図のようにθの角度をもって壁にぶつかったとき、どのくらいの勢いで反発するか考えてみましょう。

上図にあるように、壁と垂直方向に反射する力は|v1|×cosθとなります。ここで、壁と垂直方向で長さ1のベクトルをv2とします。ちなみに、垂直方向のベクトルを「法線ベクトル」と呼びます。ベクトルv2は長さが1なので|v2|は1となります。よって、

　　|v1| × cosθ＝|v1| × |v2| × cosθ

となりますが、この値はv1とv2の内積と同じです。v1とv2の内積は以下の式で簡単に求めることができます。

　　v1・v2 = v1のx成分 × v2のx成分 ＋ v1のy成分 × v2のy成分

ここまでの説明を整理しましょう。壁の法線単位ベクトルv2（壁と垂直方向の長さ1のベクトル）がわかれば、v1とv2の内積が計算できます。その値は|v1|×cosθであり、ボールが壁と垂直方向に反射する強さになります。

このように求めたベクトルを2倍して、もとの入射ベクトルと加算すれば反射のベクトルを求められます。その様子を下図に示します。

少し難しかったかもしれません。衝突判定の詳細は後述するので、この段階では「内積を使うと反射後のベクトルが簡単に求められる」ことを理解しておけば十分です。

ベクトルの外積

ベクトルの外積は“×”で表現します。計算式は以下の通りです。

　　v1×v2 = v1のx成分 × v2のy成分 ー v1のy成分 × v2のx成分

この値は以下の計算結果とも等しくなります。

　　v1×v2 = |v1| × |v2| × sinθ

内積と外積のイメージを図で表すと以下のようになります。底辺を|v2|、高さを|v1|sinθとすると、外積の計算結果はv1とv2で示される平行四辺形の面積と同じになります。

内積ではcosθを求めることができましたが、外積ではsinθを求めることができます。sinθでは0°～180°まではプラス、180°～360°までがマイナスとなります。よって、外積の計算結果の符号を見るとv1ベクトルの終点がv2の右にあるか、左にあるかといった判定が可能になります。外積が0のときsinθが0となり、θも0となります。つまり、2つのベクトルの向きが同じ＝平行ということも分かります。

衝突判定

「衝突判定は物理エンジンの肝」といっても過言ではありません。以下、色々なケースにおける衝突判定について見てゆきます。

円と円の衝突判定

円と円の衝突は三平方の定理を使って簡単に判別することができます。中心座標（x0, y0）半径r0の円と中心座標（x1, y1）半径r1の円があったとします。

この2つの円における中心座標間の距離dは三平方の定理（a²+b²=d²）より、以下の式で求めることができます。

　　（d:中心座標間の距離）² = (x1-x0)²+(y0-y1)²

　　　d=√((x1-x0))²+((y0-y1))²

後はdの値とr0とr1の合計値を比較するだけです。

（a）d ＞ r0 ＋ r1 の場合　　円は衝突していない
（b）d ＜ r0 ＋ r1 の場合　　円は衝突している

衝突している場合は、物体の向きを変更する処理を行うことになります。その計算については後述します。

円と矩形の衝突判定

円と矩形の衝突には色々な判定方法がありますが、今回の実装では以下のように判定しています。

1. 矩形の4辺の上で円の中心座標に一番近い座標を求める
2. その座標と円の中心座標までの距離を求める
3. 2で求めた距離が円の半径より小さい場合衝突していたとみなす

まず、x軸方向の中心座標を求めます。

（1）円の中心が矩形の左端より左にある場合は、矩形の左端のx座標
（2）円の中心が矩形の左右に収まる場合は、円の中心のx座標
（3）円の中心が矩形の右端より右にある場合は、矩形の右端のx座標

y軸方向の中心座標も同様に求めます。

（1）円の中心が矩形の上端より上にある場合は、矩形の上辺のy座標
（2）円の中心が矩形の上下に収まる場合は、円の中心のy座標
（3）円の中心が矩形の下端より下にある場合は、矩形の下辺のy座標

このようにして求めた矩形の4辺上の座標と円の中心座標を比較します。あとは円と円との衝突判定で行った計算と同じです。具体例を見てみましょう。円の半径をr、円の中心座標と近接点の距離をdとします。

（1）d > r →衝突していない
（2）r > d →衝突している
（3）r > d →衝突している
（4）d > r →衝突していない
（5）d > r →衝突していない
（6）r > d →衝突している

このように、円と矩形の衝突も円と円の衝突のように求めることができます。

円と線の衝突判定

この判定方法の説明は少々複雑なので結論だけ説明します※。中心座標を(x,y)とする円が速度v1で移動しているとき、線分(x0,y0)-(x1,y1)と交差する否かを判定するには以下のようなベクトル計算を行います。

円の速度をv1、線分の始点から終点へのベクトルをv2、円の中心から線分の始点へのベクトルをv0とします。v1とv2の外積をT、v0とv1の外積をTで割ったものをT1、v0とv2の外積をTで割ったものをT2と、それぞれ計算で求めます。

　　T ＝ v1 × v2
　　T1 ＝ ( v0 × v1 ) / T
　　T2 ＝ ( v0 × v2 ) / T

証明は省略しますが、T1が0から1の範囲に、かつT2が0から1の範囲に収まっていれば円は線分に衝突します。外積を計算するだけで円が線分に衝突するか否かが検出できるのです。2つの線分が交差しているか否かを判定するには、ほかにも連立方程式を使用した手法などいろいろあるようです。興味のある方は“線分の交差判定”などのキーワードで調べてみてください。衝突が検出された場合は円を反射させることになりますが、その計算については次節で説明します。

※http://marupeke296.com/COL_2D_No10_SegmentAndSegment.html
　http://stackoverflow.com/questions/563198/how-do-you-detect-where-two-line-segments-intersect

衝突時の処理

動く円と静止円の衝突

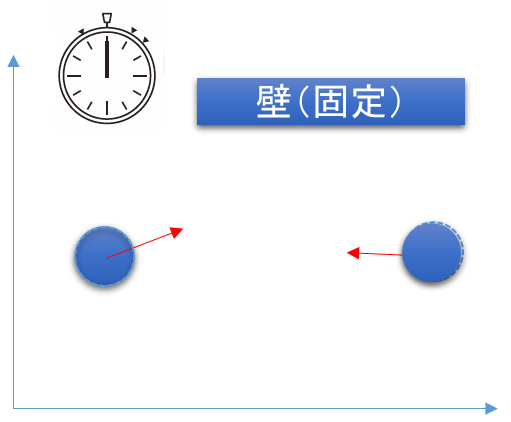
まずは片方の円が停止しているところに、別の円が衝突したケースを考えてみましょう。物理エンジンでは一定期間毎に時間を進めます。実世界では衝突した瞬間に反発しますが、物理エンジンの世界ではそうはいきません。衝突判定されたときには既に円どうしが重なり合っているので、まずは重なりを解消します。

下図のように円の中心を線で結び、その線上の反対方向に円を移動させます。片方の円が固定されている場合は反対側の円だけを、両者とも固定されていない場合は重なった距離の半分をそれぞれ移動させます。この際、質量を考慮して移動量を決定したほうがよりリアルになると思いますが、今回はシンプル最優先ということでこのような仕様にしました。

次に、衝突後に速度ベクトルがどのように変化するかを求めます。円と円だとややこしいので、停止している円を直線で近似します。直線は2つの円の中心を結ぶ線と垂直に交わり、円と接する線とします。イメージを以下に示します。

上図において、円の速度ベクトルvを入射ベクトルとします。計算で求めたいのは反射ベクトルv´です。円が反射する様子を左図に、ベクトルの様子を右図に示します。

この反射ベクトルは以下の手順で求めます。

1. 入射ベクトルの法線成分を求めます。法線とは接線と垂直に交わる線のことですが、この法線ベクトルは円の中心を結ぶことで簡単に求まります。その法線ベクトルを長さで割って（＝1/長さを掛けて）法線単位ベクトルを求めます。入射ベクトルと法線単位ベクトルの内積が求めるべきベクトルとなります。
2. 接点を始点とし、法線ベクトルを2倍します。
3. 2のベクトルと入射ベクトルを加算します。始点から終点を結ぶベクトルが反射ベクトルとなります。

このようにベクトルの内積を使うことで簡単に反射ベクトルを求めることができました。これもベクトルの内積を使うことで簡単に求めることができます。

動く円と動く円の衝突

動く円どうしが衝突したときはどのように処理するか見てゆきましょう。円Aと円Bが衝突した場合を考えてみます。円Aの速度ベクトルを接線方向の成分と法線方向の成分に分解します。同じように円Bの速度ベクトルも接線方向と法線方向に分解します。法線の求め方は“動く円と静止円の衝突”で説明しました。法線の単位ベクトルと速度ベクトルの内積を求めることで法線成分ベクトルを計算できます。

接線方向の単位ベクトルは法線単位ベクトルから簡単に求めることができます。下図にあるようにx成分とy成分を入れ替え、y成分の符号を変更するだけで垂直に交わるベクトルが求められます。三角形が合同なのでベクトルの長さも同じになります。

円Aと円Bの接線方向と法線方向のベクトルを求められたら、あとはそれぞれを加算することで円Aと円Bの衝突後のベクトルを求めることができます。

ここまでの説明を整理しましょう。

1. 円Aの速度ベクトルを接線成分Aと法線成分Aに分解
2. 円Bの速度ベクトルを接線成分Bと法線成分Bに分解
3. 円Aの衝突後の速度ベクトルは、法線成分Bと接線成分Aの合成、円Bの衝突後の速度ベクトルは接線成分Bと法線成分Aの合成

本来であれば、それぞれの円の質量や反発係数、エネルギー保存則などを考慮して計算すべきですが、今回はあくまでも入門ということでこのように割り切った仕様としました。

お疲れ様でした。ベクトルの話はここまでです。すべて理解するのは大変だったかもしれません。ただ、“ベクトルは非常に強力だ”ということは伝わったかと思います。次は、このベクトルの計算をどのようにプログラムに落とし込むかについて見てゆきます。