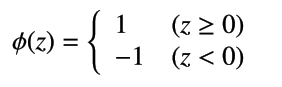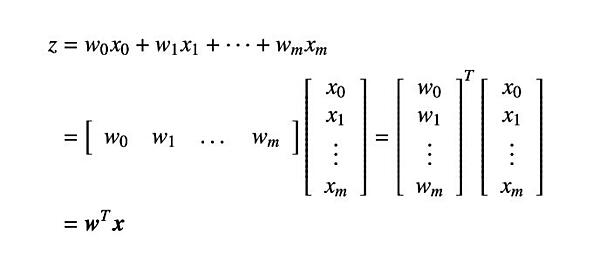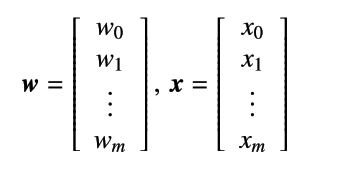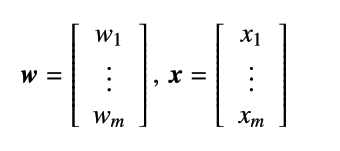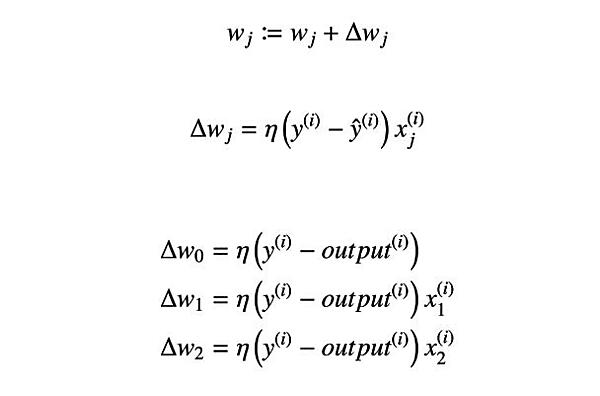原著の『Python Machine Learning』は2015年9月に米国などで発売。「機械学習の考え方」と「Pythonプログラミングによる実践」をバランスよく解説していると評価され、米国Amazon.comでベストセラー。その日本語訳はコラムや脚注、付録が追加され、2016年6月に発売されました。ここでは、本書のより効果的な活用法について監訳者が解説します。
第2章の内容
『Python機械学習プログラミング』の第2章では、パーセプトロン、ADALINE という2 つのアルゴリズムについて説明されます。本章の内容を理解することにより、機械学習の分類タスクの考え方、Python による機械学習アルゴリズム実装への習熟、最適化の考え方等について理解を深めることができます。
各節で扱われる内容を「数式を用いた説明」「Pythonによる実装」「分析結果の解釈」の3つによって大まかに分類すると、表1のようになります。
「Pythonによる実装」は、第3章以降でscikit-learnを用いて機械学習のアルゴリズムを実行するときの基礎になります。「数式による説明」は、第3章でロジスティック回帰やサポートベクトルマシンなどのアルゴリズム、また第12章でニューラルネットワークを理解するのに重要な事項です。
以上のように、第2章は本書を読み進めていく上で重要な位置付けになっています。一方で、前回記述したように、数式が最初から登場したり、クラスを用いてパーセプトロンやADALINEのアルゴリズムを実装したりと、少し取っ付きづらい面もあるかもしれません。本記事では、そうした点を補っていければと思います。
パーセプトロンの定式化
2.1節「人工ニューロン--機械学習の前史」から2.3節「Irisデータセットでのパーセプトロンモデルのトレーニング」では、数式を交えたパーセプトロンの概要、Pythonによる実装、そしてその分析結果が説明されます。
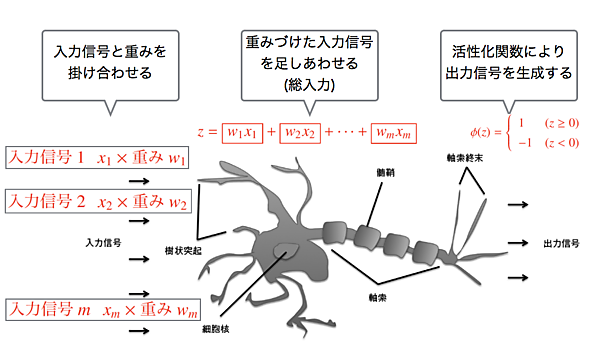
p.18の図において、入力信号がm個あるとします。以下のように図の左側には5個の矢印が描かれていますが、この1つ1つが入力信号だと考えてください。
入力信号1の信号値がx1、入力信号2の信号値がx2、・・・、入力信号mの信号値がxmであるとします。これらの入力信号は重みをw1、・・・、wmとして、それぞれを足し合わせたものが細胞核に取り込まれます。これを総入力(net input)と呼んでいます。
総入力z = (入力信号1 の重み付きの信号値) + (入力信号2 の重み付きの信号値) + … + (入力信号m の重み付きの信号値) = w1x1 + w2x2 + … + wmxm
例えば、3 つの入力信号があるとして、1 番目の入力信号の信号値をx1 = 1、2 番目の入力信号の信号値をx2 = 2、3 番目の入力信号の信号値をx3 = 3 とします。これらの入力信号の重みをw1 = 0.2、w2 = 0.4、w3 = 0.5 とします。このとき、
総入力z = (入力信号1 の重み付きの信号値) + (入力信号2 の重み付きの信号値) + … + (入力信号m の重み付きの信号値) = w1x1 + w2x2 + w3x3 = 0.2 × 1 + 0.4 × 2 + 0.5 × 3 = 0.2 + 0.8 + 1.5 = 2.5
となります。例えば、すべての入力信号の重みが1 のときの総入力は、
z = 1・x1 + 1・x2 +・・・+ 1・xm = x1 + x2 +・・・+ xm
となり、単純にすべての入力信号の信号値を足し合わせたもの(和) になります。さて、本書内でも説明されているように、Rosenblatt によるパーセプトロンは以上の神経細胞を模したアルゴリズムで、入力信号から出力信号を判定するものです。そのアイディアは、
入力信号の重み付きの和が一定値(しきい値) 以上であれば出力信号が生成される
というものです。これは、総入力z がしきい値θ を超えているかどうかを判定することにより行います。数式で表すと、次の判定条件になります。
総入力z ≥ しきい値θ
総入力z の式を具体的に代入すると、以下のようになります。
z = w1x1 + w2x2 + … + wmxm ≥ θ
先ほどの具体例では、以下のようになります。
w1x1 + w2x2 + w3x3 = 2.5 ≥ θ
例えば、θ = 2 とすると左辺はθ より大きくなります。θ = 3 とすると左辺はθ よりも小さくなります。
上記の総入力z がしきい値θ を超えるかどうかを判定する式において、右辺のθ を左辺に移行すると、以下の式を得ます。
-θ + w1x1 + w2x2 + ・・・ + wmxm ≥ 0
この式で、
-θ = w0x0
とおくと、
w0x0 + w1x1 + w2x2 + w3x3 + ・・・ + wmxm ≥ 0
となり、統一的な形で表すことができます。w0とx0の決め方は様々なものが考えられます。例えば、w0 = -1、x0 = θ としても良いですし、w0 = θ、x0 = -1 としても良さそうです。本書では、重みをw0 = -θ、x0 = 1 としています。このとき、総入力z は次式
z = w0x0 + w1x1 + ・・・ + wmxm
で表せます。総入力z が0 以上ならば出力信号が生成され、0 未満ならば出力信号が生成されません。このように、総入力z の値から出力の値を判断する活性化関数φ = φ(z) は次式で定義されます。
例えば、入力信号の重みをw0 = 0.2、w1 = 0.4、w2 = 0.5 とすると、総入力が0 以上となるのは、
z = w0x0 + w1x1 + w2x2 = 0.2・1 + 0.4・x1 + 0.5・x2 ≥ 0
となります。この式を整理すると、
x2 ≥ -0.4/0.5x1 - 0.2/0.5
となります。分数を簡潔にすると、
x2 ≥ -0.8x1 - 0.4
となります。
行列による総入力の表現
なお、総入力z の式は、行列を用いて書き表すことができます。
ここでは、以下のようにしています。
なお、p.19の式2.1.1 ではベクトルwとxは以下のように定義されています。
同じページの式 2.1.3 以降ではw、x にそれぞれw0、x0が追加されていることに注意してください。
重みを推定するための計算方法
さて、以上では入力信号の重みw0、・・・、wm は与えられるものとして扱ってきました。しかし、これらの重みは、出力信号が生成される場合と生成されない場合をうまく説明できるように調整する必要があります。Rosenblatt によるパーセプトロンは、次の手順で重みを調整していきます。
- 1. 重みを0 または値の小さい乱数で初期化する。
- 2. トレーニングサンプルx0(i) ごとに以下の手順を実行する。
- (a)出力値ŷを計算する。
- (b)重みを更新する。
- この記事のキーワード