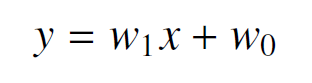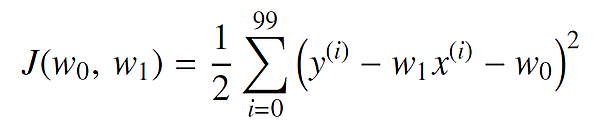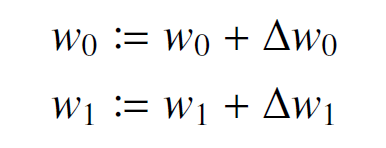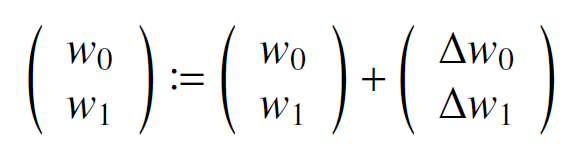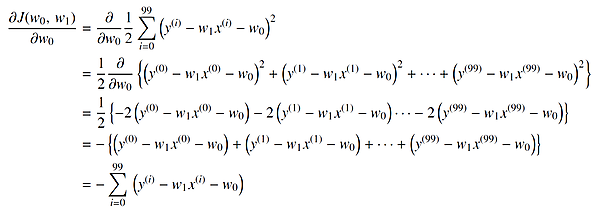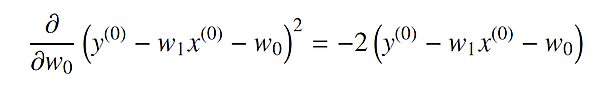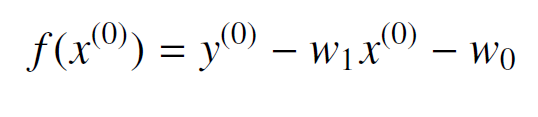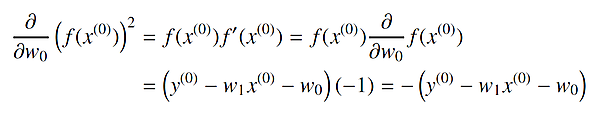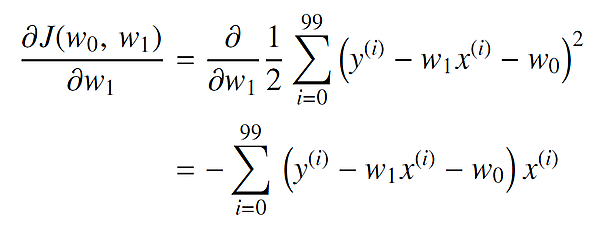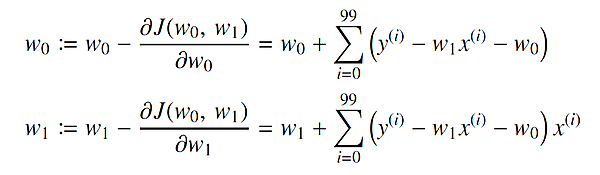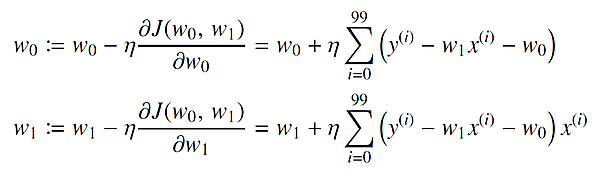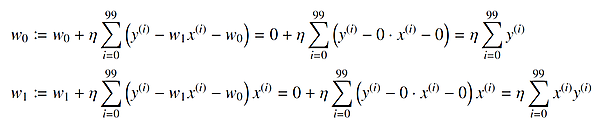ブック・インサイド『Python機械学習プログラミング』―単純な例でADALINEのイメージをつかむ

勾配降下法: 誤差平方和の勾配と逆方向に重みをずらしていく

ここでは、勾配降下法を用いて重みの更新を行いながら、最適な重みの値に近づけていきます。本書では、一般的な記法で記述されていますが、ここでは簡単な例で説明します。Irisデータセットの品種がsetosaまたはversicolorの100サンプルについて、2番目の特徴量（Petal-Length）と品種（setosaまたはversicolor）の関係を説明します。xをPetal-Length、yを品種（setosaのとき-1、versicolorのとき1）として、これらの関係を次の式で表します。この式のw₁は傾き、w₀は切片です。

w₀、w₁の最適値を勾配降下法を用いて求めてみましょう。この場合、以下の式が最小となるw₁、w₀を推定します。

この例の場合は、最小二乗法などを用いて、解析的に J(w₀, w₁ ) を最小化するw₀、w₁を求めることができます。しかし、ここではそうしたアプローチを行うのではなく、w₀、w₁を少しずつ変化させながら収束させていく方法をとってみましょう。そのために、以下の式により重みw₀、w₁の更新処理を繰り返していきます。

Δw₀、Δw₁は重みの更新の大きさを表しています。これらの式をまとめると、次のように行列を用いて表すこともできます。

更新の大きさΔw₀、Δw₁はどのように決めればよいのでしょうか。勾配降下法では「誤差平方和の勾配方向」にとります。誤差平方和の勾配とは、「誤差平方和 J(w₀, w₁ ) の w₀、w₁に関する偏導関数」となります。w₀に関する偏導関数は、次式のようになります。

2行目から3行目の変形では、例えば、次の関係を用いています。

わかりにくい場合は、まず次の式をおきます。

この式に対して、連鎖律を使って次のように変形するとよいかもしれません。

同様にして、w₁に関する偏導関数は、次のようになります。

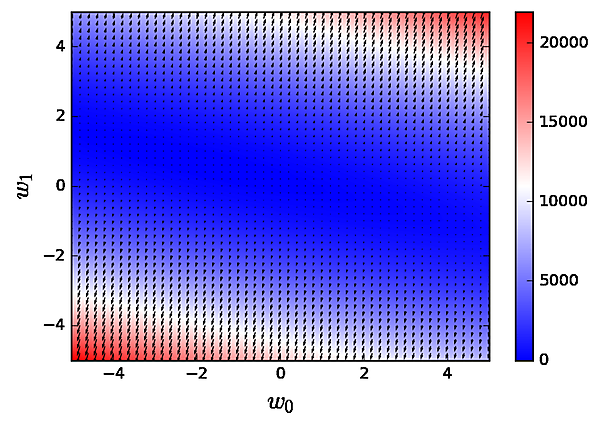
図2-2 は、w₀、w₁ともに − 5 から 5 までで 0.01 刻みで点を取ったときに誤差の値をプロットしています。また、各点における勾配の向きと大きさをベクトルで表しています。

図2-2：誤差とその勾配。横軸：w₀、縦軸：w₁

図2-2 を見ると、図の左側のやや上側付近から右側のやや下側付近にかけて青色が濃い領域が存在していることを確認できます。この領域では、誤差および勾配が小さくなっていることを確認できます。

勾配降下法では、誤差を最小化するために、それぞれの重みにおいて誤差が最も小さくなる方向に重みをずらしていく処理を繰り返していきます。誤差が最も小さくなる方向とは、勾配の逆方向です。したがって、先ほど求めた∂J(w₀, w₁ ) ⁄ ∂w₀、∂J(w₀, w₁ ) ⁄ ∂w₁にマイナスをつけた−∂J(w₀, w₁ ) ⁄ ∂w₀、−∂J(w₀, w₁ ) ⁄ ∂w₁によって、w₀、w₁を更新します。よって、次の式で更新することになります。

さらに、学習率というパラメータを導入します。学習率は、「どの程度勾配の逆方向にずらすか」を表すパラメータです。学習率を η とすると、w₀、w₁の更新ルールは次式のように表されます。

例えば、重みw₀、w₁の初期値を w₀ = 0、w₁ = 0 と設定します。このとき、1 回目の重みの更新は、次式により行われます。