偏差(ズレ)を小さくしてみよう
偏差(ズレ)を小さくしてみよう
P動作をとりこむことで、モーターの回転角度制御はON/OFF制御に比べて格段によくなりましたが、定常偏差が残ってしまうことがわかりました。この定常偏差が無視できる場合にはこのままでもよいのですが、無視できない場合には取り除く必要があります。今回も、90度に安定させるため、定常偏差を取り除くことにします。
定常偏差をなくすためにはどうすればよいでしょうか。この実験の場合、P動作の定常偏差は、1回の制御で与える制御量(回転速度)が小さくなりすぎて、実際にモーターを動かすのに必要な量に到達しないことが原因でした。それなら、この小さな制御量を、モーターを動かすのに必要な力になるまで蓄積する=モーターが実際に回転する程度の回転速度になるような量まで偏差を蓄積してみてはどうでしょう。
つまり、時間経過に応じて偏差量を積算していくと、いつかはモーターを動かすことができる値になり、目標値に向かって動きだすというわけです。式に直すと次のようになります。
- 現在の偏差量 = (90度 - 現在のモーターの角度)× 時間間隔
- 現在の偏差量の積算値 = 前回の偏差量の積算値 + 現在の偏差量
- 現在のモーターの回転速度 = 定数 × 偏差量の積算値
偏差量は、時間間隔(積算する単位時間)あたりの偏差です。現在の偏差量の積算値は、前回の積算値に、今求めた現在の偏差量を加えたもので、処理を繰り返す中で徐々に蓄積されていきます。モーターの回転速度はこの偏差量の積算値に比例していて、偏差量の積算値に定数をかけて求めるようにしています。定数は実験をしてちょうどよい値を求めます。この回転速度が実際に回転する程度まで到達すれば、P動作の定常偏差を是正してくれるように動作するわけです。
先ほどのP動作の処理に加えてこの式をプログラムに反映して実行してみました。このときのモーターの動きは図10のようになりました。
|
|
| 図10:モーターの動き(PI動作) |
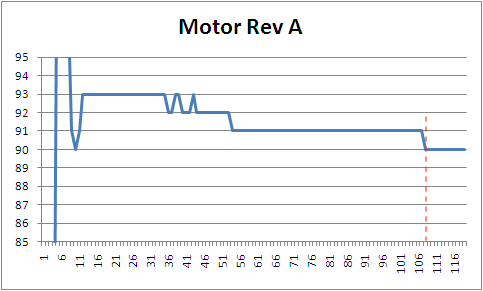
モーターの回転角度の変化をグラフに表すと図11のようになります。
|
|
| 図11:モーターの回転角度の変化(PI動作) |
再び90度付近を拡大してみてみましょう。
|
|
| 図12:モーターの回転角度の変化(PI動作)の拡大図 |
ちょっと見にくいですが、開始から5秒後程度経過した所で、ぴったり目標値の90度になっています。目標値に到達するまでに少し時間はかかりますが、目標値ぴったりに制御できました。このような制御方法を、偏差量を時間経過と共に積算して制御量を変えるため「積分制御」または「積分動作」と呼びます。そして、この制御動作のことを、積分(インテグラル:Integral)の頭文字をとって「I動作」と呼びます。
応答を早くしてみよう
I動作によって、目標値にぴったり合わせることができるようになりましたが、目標値に到達するのに少し時間がかかってしまっています。もっと早く目標値に近づけたい場合には、どうすればよいでしょうか。
I動作では、一定時間の偏差を蓄積していましたが、偏差が大きい段階と偏差が小さくなってきている段階を同じように扱っていました。しかし実際には偏差が大きい段階では大きく制御を加え、偏差が小さくなってきた段階では細やかな制御に抑えるようにしたほうが効果的なはずです。そのためには偏差が増えつつあるのか、減りつつあるのかを予測して、制御量を決めればよさそうです。
偏差が増えつつあるのか、減りつつあるのかというのは、偏差量の傾きを知ることでわかります。具体的には、ある時間間隔で、前回の偏差量と今の偏差量の差を計算して、その時間間隔で割ることで、時間間隔あたりの傾きがわかります。この偏差量の傾きが大きいときには大きく制御し、偏差量の傾きが小さいときには小さく制御すれば、目標値に到達する時間を早くすることができるでしょう。
- 偏差量の傾き = (前回の偏差量 - 今回の偏差量)/ 時間間隔
- 現在のモーターの回転速度 = 定数 × 偏差量の傾き
偏差量はI動作のときと同様、時間間隔(積算する単位時間)あたりの偏差です。偏差量の傾きを求めるために、ある時間間隔の始まりの偏差量(前回の偏差量)と終わりの偏差量(今回の偏差量)がどのくらい変わっているかを求めたいので、差をとって時間間隔で割っています。
偏差量の傾きが大きいとき(大きく変化しているとき)には大きく、偏差量の傾きが小さいとき(変化が小さくなってきているとき)には小さくしたいということですから、モーターの回転速度は偏差量の傾きに比例するように、偏差量の傾きに定数をかけて求めています。定数は実験をしてちょうどよい値を求めます。これで、I動作で目標値に近づくまでにかかっていた時間が短くなるはずです。
先ほどのPI動作の処理に加えてこの式をプログラムに反映して実行してみました。このときのモーターの動きは図13のようになりました。
|
|
| 図13:モーターの動き(PID動作) |
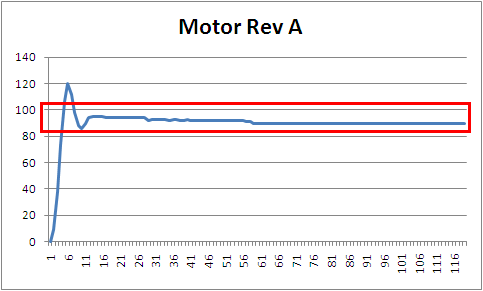
モーターの回転角度の変化をグラフに表すと図14のようになります。
|
|
| 図14:モーターの回転角度の変化(PID動作) |
再び90度付近を拡大してみてみましょう。
|
|
| 図15:モーターの回転角度の変化(PID動作)の拡大図 |
90度にぴったり合うまでの時間が3秒程度になり、I動作のときと比べて応答が早くなったことがわかります。このような制御方法を、偏差量の傾きを計算して制御量を変えるため「微分制御」または「微分動作」と呼びます。そして、この制御動作のことを、微分(デリバティブ:Derivative)の頭文字をとって「D動作」と呼びます。
今回は、2輪倒立振子ロボットの走りの違いから、ON/OFF制御や、PID制御について考えました。次回は、2輪倒立振子の走行にPID制御の考え方を適用してみましょう。