はじめに
前回は、不正/正当な取引を予測する機械学習モデルの仕組みとして、予測するためのデータから数百の特徴を活用し、決済が不正かどうかを確率(またはスコア)で出力する不正使用分類器について解説しました。
今回は、この分類器のモデルが「どのくらい効果的であるか」を判断する仕組みについて解説します。
評価における重要語句
機械学習システムの評価手法をより理解するにあたって、いくつかの重要語句を定義しておきます。
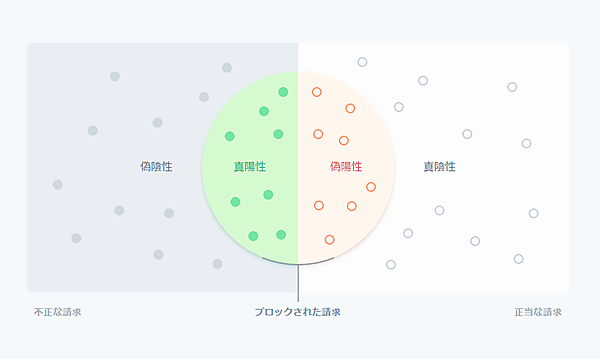
機械学習モデルが各取引に対して、「不正使用の確率0.7超(これをP(不正使用)>0.7と書きます)と判断した際に、この決済をブロックする」という方針を立てたとしましょう。ここで、このモデルと方針のパフォーマンスを推論するのに役立つ重要語句(数値)は下図のとおりです。
- 適合率:方針の適合率とは、ブロックした取引のうち実際に不正使用であったものの割合を指します。適合率が高いほど偽陽性が少なくなります。例えば10件の取引中6件がP(不正使用)>0.7で、そのうち実際に不正だった取引が4件だったとします。その場合の適合率は4/6=0.66となります。
- 再現率:感度または真陽性率としても知られますが、再現率とは方針によって把捉されたすべての不正使用の割合(P(不正使用)>0.7と判定された不正使用の割合)を指します。再現率が高いほど偽陰性は少なくなります。仮に10件の取引で5件が実際に不正使用だったとして、モデルがそのうち4件にP(不正使用)>0.7を割り当てた場合の再現率は4/5=0.8となります。
- 偽陽性率:偽陽性率とは方針により誤ってブロックされたすべての正当な決済の割合です。仮に10件の取引で5件が正当なものだったとして、モデルがそのうち2件にP(不正使用)>0.7を割り当てた場合の偽陽性率は2/5=0.4になります。
分類器の評価に用いられる数値は他にもありますが、ここでは以上のものに集中することとします。
適合率-再現率曲線およびROC曲線
では、適合率や再現率、偽陽性率はどのような数値が望ましいのでしょうか。理論上、適合率は1.0(不正使用のクラスに分類された取引のすべてが実際に不正使用である)、偽陽性率は0(誤って不正使用クラスに分類した正当な取引は1つもない)、再現率は1.0(すべての不正使用が不正使用であると特定されている)となります。
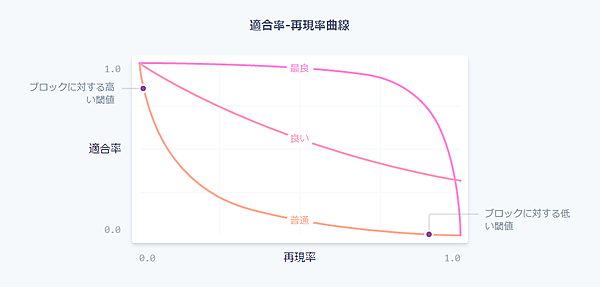
しかし、実際のところ適合率と再現率には常にトレードオフが存在します。ブロックに関する確率閾値を引き上げれば適合率は上昇し(ブロックの基準がより厳格になったため)、再現率は減少します(高い確率基準に合致する取引が少なくなるため)。確率閾値を引き下げれば、基本的に逆のこと(適合率が下降し、再現率は上昇)が起きます。モデルにおいて閾値を変化させたときの適合率と再現率のトレードオフは、「適合率-再現率曲線」により表されます(下図)。
モデルは不正使用の特徴を追加したり、他のモデルのパラメータを調整したり、さらにStripeネットワーク全体から得られるデータをトレーニングデータとすることで、より優れたものになっていきます。それに伴い、適合率-再現率曲線もまた、上図に示したように変化していきます。モデルはStripe上の多数の事業に対するトレードオフを統制するものであり、データサイエンティストと機械学習エンジニアでモデルを修正する際には適合率-再現率曲線への影響を詳細にモニタリングします。
適合率-再現率曲線グラフを参照する際は2つのパフォーマンス概念を理解しなければなりません。一般的にグラフの右上(適合率と再現率ともに1.0になるところ)近くにあるほどモデルは優れていると言えます。しかし、モデルを運用化する際には適合率-再現率曲線上のどこかに操業点を置く必要が出てきます(Stripeのケースでは取引ブロックに関わる方針閾値となる)。こうした選択を通じてモデルの活用が事業に及ぼす影響を制御するのです。
ここで、単純に言うと2つの問題があります。正しい特徴を追加し、優れた機械学習モデルを作成するというデータサイエンス問題と、機械学習モデルを出力する方針の選択というビジネス問題です。データサイエンスは適合率-再現率曲線の形状を制御し、ビジネス問題は曲線状のどこで事業を操業するかを制御します。
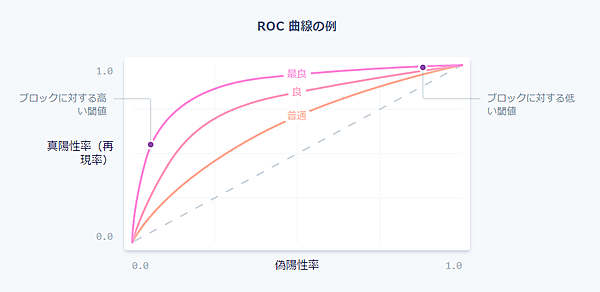
機械学習モデルを評価する際に検討する別の曲線としてROC曲線があります。ROCとはReceiver Operating Characteristic(受信者動作特性)の略で、同曲線がもともと信号処理に用いられていたことが由来です。ROC曲線は偽陽性率(X軸)と真陽性率(Y軸。これは再現率と同じ)を様々な方針の閾値に対しプロットしたものです(下図)。
理想的なROC曲線はグラフの左上(再現率が1.0、偽陽性率が0.0)近辺にあり、モデルが改善されるにつれて、さらに左上に近づいていきます。モデル全体の品質を測る方法としてはROC曲線下面積(またはAUC)を算出します。理想的なケースのAUCは1.0になります。モデルを開発する際には適合率-再現率曲線やROC曲線、AUCがどのように変化するかを注視します。スコア分布
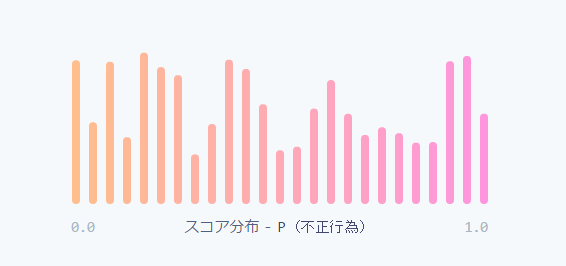
取引に対して不正使用確率を0.0〜1.0の値でランダムに割り当てるモデルがあるとします。これでは正当な取引と不正な取引とを区別できないため意味がありません。こうしたランダム性はモデルのスコア分布、つまり可能性のあるスコアを獲得する割合によって示されます。完全にランダムな場合のスコア分布はほぼ一様になるでしょう(下図)。
モデルが不正使用に関する予測能力をまったく持たない場合のスコア分布は上図のように一様なものとなりますが、特徴を追加し、トレーニングデータを用いることで不正/正当取引の判別能力は向上し、スコア分布も双峰性が高まります。つまり0.0と1.0の周辺にピークが表れてくるでしょう(下図)。
双峰性自体はモデルの優劣と直接的な関係はありません。例えばランダムに0.0と1.0の確率を割り当てるようなモデルでも同じようなスコア分布になります。しかし「低スコアの取引は正当、高スコアの取引は不正である」とする実証データが存在するならば、双峰性の高い分布はモデル効率改善の兆候になります。
適合率と再現率の算出
適合率と再現率は異なる場面で算出されます。モデルのトレーニング中にモデル開発に利用している履歴値を活用する場合と、モデル開発の後に本番環境のデータ(実際にモデルを使って不正使用をブロックした際に得られるデータ)を活用する場合です。
前者の場合、データサイエンティストはトレーニングデータの一部をトレーニングセットに、それ以外を検証セットに割り当てることがよく行われています。例えば最初の80%をトレーニングセットに、残りの20%を検証セットにするといった具合です。
トレーニングセットはモデルを作成するための機械学習機能に適用するデータです。モデルが準備できたら、検証セットの中にあるサンプルデータにスコアを割り当てられるようになります。検証セットのスコアはその出力値と合わせてROC曲線や適合率-再現率曲線、スコア分布の算出などにも活用されます。
データはトレーニングセットと検証セットに分割しますが、これは作成したモデルの予測力を正確に計測するためです。トレーニングセットはモデルのトレーニングで使用済みのため、新規データに対するパフォーマンスよりも優れています。そこで検証セットでテストすることでモデルの検証がより正確なものになるのです。
検証セットでテストした結果、「モデルが効果的である」と判断されると本番環境へ導入します。本番環境では、次に「モデルと方針のパフォーマンスをどう継続的にモニタリングするか」という問題が出てきます。ブロックされなかった不正な決済はカード保有者からの訴えなどにより反応を測定できますが、ブロックした決済は「万一ブロックしなかった場合にどんな問題が発生していたか」を窺い知ることができません。本番環境における適合率-再現率曲線ないしROC曲線を完璧に算出するには、こうした反実仮想分析が関わってくるため検証曲線の算出よりも複雑になります。ブロックされた決済が万一ブロックされなかった場合にどうなっていたかの統計的な推定値を定める必要があります。Stripeではそのための方法を開発していますが、詳細はこちらのセッションを参考にしてください。
ここまで、データサイエンティストが機械学習モデルの開発時にチェックするいくつかの測定値を説明してきました。次は、事業側が不正使用を予防するためにどのような考え方をすべきか説明します。これまで検討してきた多くの内容(例えば適合率と再現率の相反関係など)は不正使用が皆さんの事業にどのような影響を及ぼすかを把握するのに役立つはずです。
不正使用防止システムパフォーマンスの推論
時に不正使用予防プラットフォームの効率は1つの数字でしか表されないことがあります。しかし1つの数字に固執するのは事業にとって最適とは言えない結論に至る可能性があります。不正使用担当チームが持つ数字は不正使用関連のものばかりであるためです。不正使用担当チームには収益損失の責任はありませんし、収益損失は不正使用損失よりも特定が難しいでしょう。
以下に、偽陽性-偽陰性(ないし適合率ー再現率)トレードオフの現実世界における影響をいくつか示します。
- もし訴訟やクレームといった紛争を起こさないことだけを考えるならば、すべての決済をブロックしてしまえばゼロまで引き下げられるでしょう。これでは事業が成り立たないので実際にはあり得ませんが、このようなモデルを使えば不正使用だけでなく正当な取引もすべてブロックするため、目も当てられない偽陽性率になってしまうことでしょう。
- 他の要素を考えず、低い偽陽性率だけに固執するのも危険です。どんな不正使用をもブロックしなければ偽陽性率は確実にゼロになりますが、いくら偽陽性率が低くても紛争率が1%に近くなれば何も意味がありません(これはほとんどのカードネットワーク全体で設定されています)。そうなると多くの偽陽性に繋がるとしても不正使用を大幅に削減しなければなりません。
上記の例は机上の空論に思えるかもしれませんが、事業は時に偽陰性を過剰評価し、偽陽性を過小評価することが分かっています(見逃した不正使用に対して敏感になる)。この結果、例えば国際的なカードや特定領域のIPアドレス、あるタイプのカードをすべてブロックするなどの強引な対応を行うことがあります。機械学習システムはこのような処理に対して免疫があります。手動で行うラベリングに頼っているシステムでは、このような処理を再現する学習をしてしまいます。Stripeではすべての訴訟やクレーム情報をカードネットワークとカード発行者から直接収集しているので、Radarにとって問題になりません。
システムの有効性と関係する例をもう1つ紹介します。皆さんの不正使用防止システムは、本当に収益につながっているでしょうか。多数の不正使用を見つけていても、正しい取引が多数ブロックされているとしたら、機会損失になっているかもしれません。
単純な例で計算してみましょう。生産に400円かかる製品を1000円で販売しているとします。正当な販売では利潤は600円です。一方、不正な取引は400円(生産費)にチャージバック手数料1,500円を加えた計1900円の損失になります。
これらの数字を鑑みると、不正な取引を1件回避できるならば1900円/600円=3.17件の正当な取引を諦めることもあり得ます。別の見方をすれば、ブロックする3.17件の取引のうち確実に1件が不正使用である限り、不正使用検出システムによって利潤が上昇します。この単純な例では、1/(1+3.17)=0.24が損益分岐適合率です。このシステムの適合率が0.24未満ならば、同システムの利用は収益を減らしているのです(チャージバック率が低減されているとしても)。
チャージバック率の上限である1%に近づいている際は損益分岐値を下回る適合率を容認しなければならない時もあるかもしれません。しかし本当に考えるべきは「多数のパフォーマンス測定値がどういった関係にあるのか」と「特定の状況を実現するために正しいトレードオフがどこにあるか」の2点です。
さまざまなルールと手動のレビューでパフォーマンスを改善
Radarでは自動的な機械学習アルゴリズムに加えて、個々の事業者が個別にカスタマイズしたルール(IPアドレスの国とカード発行国が異なる場合の10万円を超える取引はすべてブロックなど)を設計し、フラグが付いた決済をダッシュボードの中でレビューできます。
こうしたルールはシンプルなモデルと見なすことができます。適合率と再現率のトレードオフを十分に考慮しつつ、モデルと同じ方法で評価対象とすべきです。Radarを活用してルールを設計した場合、クレームや訴訟、払い戻しになった場合に統計履歴を提示し、必要な情報を提供します。
同じく重要な点ですが、ルール(事業特有のロジック)や手動レビューは利用者側で適合率ー再現率曲線の形状を理想的な形に変化させられるようになります。
機械学習アルゴリズムが事業に特定の不正使用を見逃している場合、それらを自動的にブロックするルールを設計することもできます。そうした具体的な介入は適合率への負担がほとんどないまま再現率を上昇させ、好ましい適合率-再現率曲線上で操業点を動かせるようになります。
また、取引中の一部のクラスを全面的にブロックする代わりに手動レビューへ回すことで、再現率への影響なしに適合率を向上できます。同様に一部の取引を全面的に許容する代わりに手動レビューへ回すことで、適合率への影響なしに再現率を向上できます。
もちろんこうしたメリットを得るにはマンパワーが必要になります。しかし手動レビューやルールが追加できることで、不正使用の除外をさらに最適化できるようになります。
おわりに
本連載がStripeにおける不正使用予防に対する機械学習の応用や、皆さんの事業における不正使用検出システムの効率的な測定方法の理解に役立てば幸いです。「Radarについてもっと知りたい」という場合はドキュメントを参照してください。