はじめに
前回は「線形代数への招待」と題して、機械学習における線形代数の世界を覗いてみました。そこでは線形代数は「表記」としての役割を担い、例えばベクトル・行列を用いることで積と和を多用する数式(これまでのニューロンの入出力関係を思い出して!)を非常にシンプルな形でまとめることができましたね。
今回も、引き続き線形代数をテーマに機械学習の世界を見ていきます。今回は連立方程式を行列操作で解くことを考えます。連立方程式とは、皆さんも中学生の時に学んだあの連立方程式のことです。果たしてどのように機械学習の世界につながっていくのでしょうか?
行列の操作で連立方程式を解くってどういうこと?
そもそも「行列を用いて連立方程式を解く」とは、どういうことでしょうか。中学数学の定番問題を用いて考えてみます。
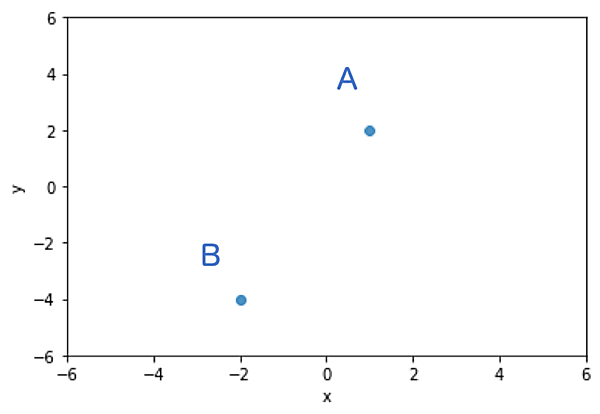
図1のような2点$A(1,2)$, $B(-2,-4)$を通る直線を求めてみましょう。
直線の式は$y=ax+b$という形で表すことができるので、次のように、この式に各点を代入すれば良いですね(式1)。
$$\left\{ \begin{array}{ll} a + b = 2 \\ -2a + b = -4 \end{array} \right.$$$a$,$b$という2つの未知数がある状況で(異なる)2つの方程式があるので、この連立方程式は消去法を用いて素直に解くことができます。解は$a = 2$, $b = 0$となります。
別の解法を考えてみましょう。式1を行列とベクトルを使って表現してみるのです。これまでと同様のシンプルな数式が得られるでしょうか。まず左辺の係数をまとめた $A = \begin{pmatrix} 1 & 1 \\ -2 & 1 \end{pmatrix} $ を考え、さらに未知数をまとめた $x = \begin{pmatrix} a \\ b \end{pmatrix} $ 、及び右辺の値をまとめた $b = \begin{pmatrix} 2 \\ -4 \end{pmatrix} $ を定義します。すると、式1は次のような形になります(式2)
$$Ax = b$$
さすが線形代数。これまでに説明してきた通り数式がとてもスッキリしますね。では、式2を用いて求めたい未知数$a$,$b$、つまり$x$を求めることを考えてみましょう。
実はこれ、行列操作を用いればとても簡単なのです。$A$の逆行列$A^{ -1 }$というものを式2の両辺に掛けてあげれば、一発で求められます。逆行列とは、2や3といった通常の数字における逆数に対応するものです。例えば、2の逆数は$\frac{ 1 }{ 2 }$です。つまり元の数字にかけると1を作ることができる数字のことですね。線形代数の世界では、元の数字にかけると単位行列$E$(対角成分が全て1でそれ以外の成分が全て0であるような行列)が得られる、そんな行列のことを逆行列と呼びます。逆行列は通常の数字と異なりいつでも存在するわけではありませんが、今回の場合は $A^{ -1 } = \frac{ 1 }{ 3 } \begin{pmatrix} 1 & -1 \\ 2 & 1 \end{pmatrix} $ です(逆行列の存在条件に興味がある方は「行列式」を調べてみてください)。$A$の逆行列$A^{ -1 }$を式2の左から掛けると、
$$x = A^{ -1 } b = \frac{ 1 }{ 3 } \begin{pmatrix} 1 & -1 \\ 2 & 1 \end{pmatrix} \begin{pmatrix} 2 \\ -4 \end{pmatrix} = \begin{pmatrix} 2 \\ 0 \end{pmatrix} \Biggl( = \begin{pmatrix} a \\ b \end{pmatrix} \Biggr)$$となります($A^{ -1 } Ax = Ex = x$であることに注意)。当然、消去法を用いた場合と同じ結果になっていますね!
データが1つ増えると、状況がガラリと変わる
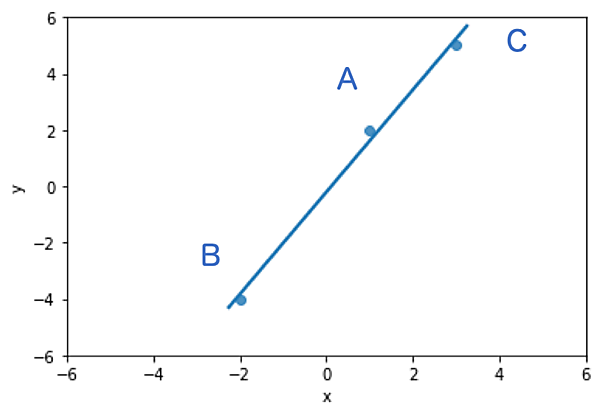
ここで、今の状況に少し変化を加えます。これから急速に機械学習の世界に近づいていきますよ。何をするかというと、新たにもう1点$C(3,5)$というデータが与えられた場合を考えるのです。引き続きこれら3点A,B,Cを通るような直線を考えてみます。直線の式はやはり$y = ax + b$なので、次のような3つの方程式が得られます(式3)。
$$\left\{ \begin{array}{ll} a + b = 2 \\ -2a + b = -4 \\ 3a + b = 5 \end{array} \right.$$
ここで、 $\Phi = \begin{pmatrix} 1 & 1 \\ -2 & 1 \\ 3 &1 \end{pmatrix}$, $x = \begin{pmatrix} a \\ b \\ \end{pmatrix}$, $c = \begin{pmatrix} 2 \\ -4 \\ 5 \end{pmatrix}$ を定めると、次のようになります(式4)。
$$\Phi x = c$$式4は一見すると式2を解いたときと同じように$\Phi$の逆行列を求めれば解けそうですね。しかし、残念ながら$\Phi$は逆行列を取ることができないのです。そもそも逆行列は正方行列、つまり行と列の数が同じ行列でないと考えることができません。「それじゃ、消去法で解いてみよう!」と意気込んでやってみるのですが、残念ながらこれも解けません。試しに2つの式を使って$a$,$b$の値を求めてみてください。$a$,$b$を使わなかった残りの方程式に代入すると、その方程式が成り立たないことがわかると思います。
未知数の個数よりもデータの数が多い時、
解は存在しない
2点$A(1,2)$, $B(-2,-4)$だけが与えられていたときには解けていた問題が、3点目が与えられると解けなくなってしまいました。このような状況になってしまった理由は明確です。
からです。最近はビッグデータが流行っており、データは多ければ多いほど良いように思えますが、今回の結果はその感覚に反してしまいますね。
でも、直線で表すことを諦めて、例えば$y = ax^{ 2 } + bx + c$といった未知数が3つ存在するような式でデータを表すことは可能です(こうすると3点を完全に通る式を得られます)。しかし、いかにも直線で表現できそうな状況で二次関数のような曲線を選択するには少し懸念があります。「3点を通る直線を求める」ということは、どうやらとても難しいことのようです。
しかし、ここで諦めないのが数学なのです。考え方を少しだけ変えていきます。「3点を綺麗に通る直線を求める」ということはやめて、「この3点の関係性を最も上手く表現するような直線を求める」というアプローチを取ります。ある程度、妥協をするのです。そして、その手法の1つがこれまでも何度か出てきた「最小二乗法」なのです。
数式を用いた詳しい説明は各種書籍に任せますが、最小二乗法の考え方を簡潔にいうと「データ点と直線との間の二乗誤差がなるべく小さくなるように未知数を定める」というものです。図2は最小二乗法を用いて求めた「最も上手い」直線です。描かれた直線は点の真上を通ってはいないものの、「最も上手く」直線が引けていると思いませんか?
機械学習ではこのような考え方を頻繁に用います。大量にあるデータに、パラメータ数をある程度に抑えてモデルが複雑になりすぎないように工夫します(今回でいうと二次関数なら完全に表現できる3つのデータを、あえて直線の枠組みで考える)。「数学とは厳密なものだ」という印象をお持ちの方が多いと思いますが、数学という学問は時にあえて制限をかけることで、その制限の範囲内の最良の結果を求めようとします。「解けない」よりも「多少誤差が含まれているけれど解ける」の方が、物事が前に進みそうですよね。
おわりに
筆者が「解がない」という驚きに遭遇したのは、高校生の頃だったと思います。問題の答えを見て「解はない」と書いてあるのです。「そんなのずるい…」と何がずるいのかよく分からない感想を抱いたことを覚えていますが、実際にはそういう状況の方が多いものです。データサイエンスという世界に携わる今日この頃は『なるほどこの世界の方程式とは、往々にして厳密な解は得られないのだな』ということをしみじみ感じます。
さて次回は、少しだけ抽象度が上がります。テーマは「写像」。このあたりの内容は「何に使えるのか?」がなかなか実感しにくく、苦手意識がある方も多いかと思いますが、機械学習と写像には密接な関係があります。いえ、密接どころではありません。機械学習とは写像を作り上げるプロセスそのものなのです。どういうことでしょうか。次回のお楽しみです!