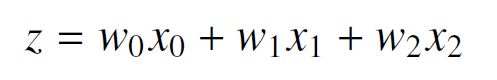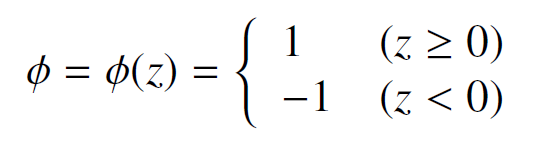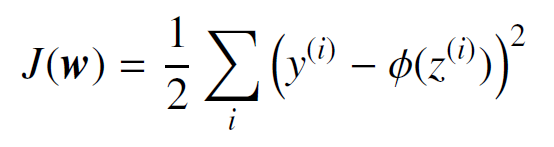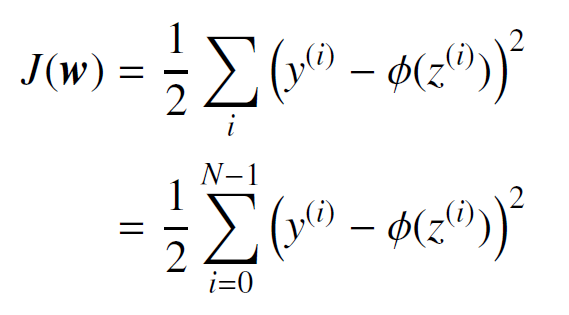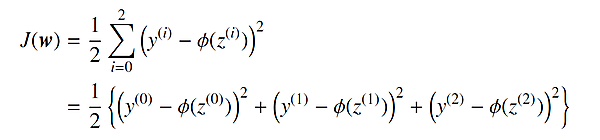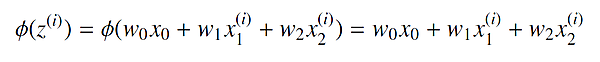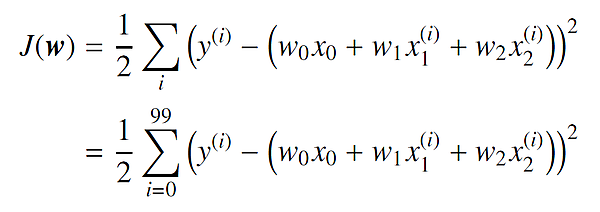ブック・インサイド『Python機械学習プログラミング』―単純な例でADALINEのイメージをつかむ

Python機械学習プログラミング
達人データサイエンティストによる理論と実践

機械学習をPythonで実装できる！

原著の『Python Machine Learning』は2015年9月に米国などで発売。「機械学習の考え方」と「Pythonプログラミングによる実践」をバランスよく解説していると評価され、米国Amazon.comでベストセラー。その日本語訳はコラムや脚注、付録が追加され、2016年6月に発売されました。ここでは、本書のより効果的な活用法について監訳者が解説します。

ADALINE

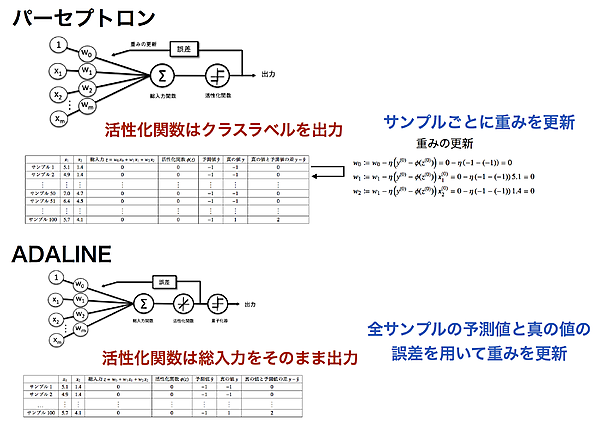
本書の2章では、「ADALINEと学習の収束」から「大規模な機械学習と確率的勾配降下法」（2.4～2.6節）の中で、ADALINE（ADAptive LInear NEuron）というアルゴリズムが扱われます。前回説明したパーセプトロンとADALINEの主な違いは、図2-1のようにまとめられます。

図2-1：パーセプトロンと ADALINE の相違点

■活性化関数の出力
パーセプトロンの活性化関数は、総入力をクラスを表す数値に変換しますが、ADALINEの活性化関数の出力は総入力そのものになります。

■重みの更新
パーセプトロンは重みをサンプルごとに更新しますが、ADALINEは全サンプルに対して更新します。

ここでは、ADALINEについてより詳しく補足的な解説を行っていきます。

誤差平方和：真の値と予測値の差を2乗して足し合わせる

パーセプトロンでは、総入力zを各入力信号に重みをかけて足し合わせたものとして計算していました。例えば、入力信号が2つの場合（x₁とx₂）、総入力zを次式で定めていました（w₀は定数項のため、x₀ = 1）。

また、出力については、総入力が0以上かどうかを判定して、総入力が0以上の場合はクラス1を、総入力が0未満の場合はクラス-1を割り当てていました。すなわち、次式の活性化関数を定義していました。

ADALINEで使用される誤差は、誤差平方和（Sum of Squared Error : SSE）です。誤差平方和は、「各サンプルの真の値と予測値の差（残差）を2乗したものをすべてのサンプルに対して足し合わせたもの」です。つまり、誤差平方和が大きいほどサンプル全体として真の値と予測値の差が平均的に大きいことになります。i 番目のサンプルの真の値を y⁽ⁱ⁾、予測値を φ(z⁽ⁱ⁾) とすると、誤差平方和は次式で表されます。

N個のサンプルのインデックスを i = 0 から i = N − 1 までとすると、上式は以下のように表すことができます。

例えば、N = 3 の場合（サンプルが3個）では、以下のようになります。

パーセプトロンで扱った例の場合、i 番目のサンプルに対して活性化関数の出力は、次のとおりです。

したがって、誤差平方和は 1 番目から 100 番目までのサンプルの真の値と予測値の差 （残差）を 2 乗して足し合わせたものになります。したがって、誤差平方和は次のとおりです。

この誤差平方和が小さくなれば、真の値と予測値は平均的に近くなります。このような重み w₀、w₁、w₂を探す必要があります。