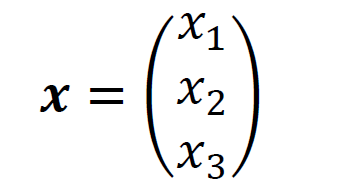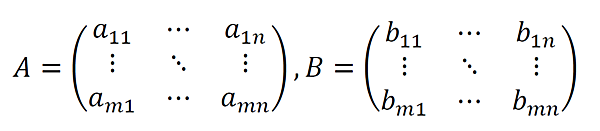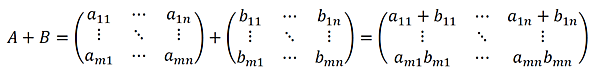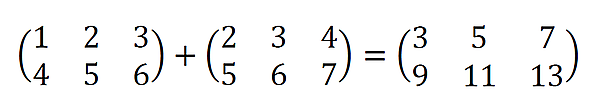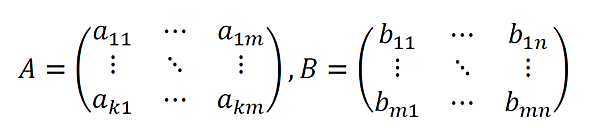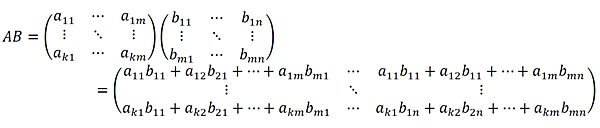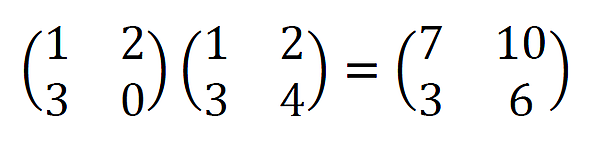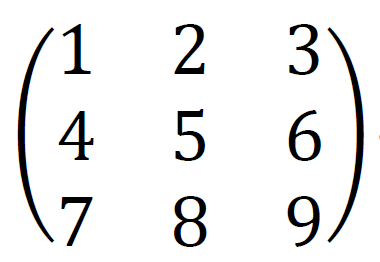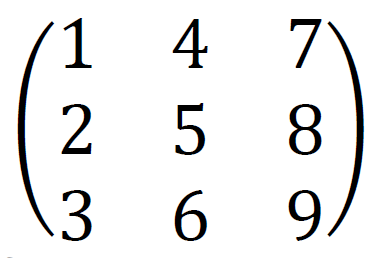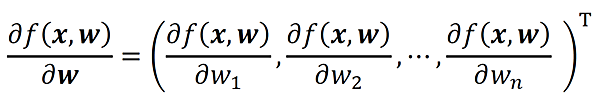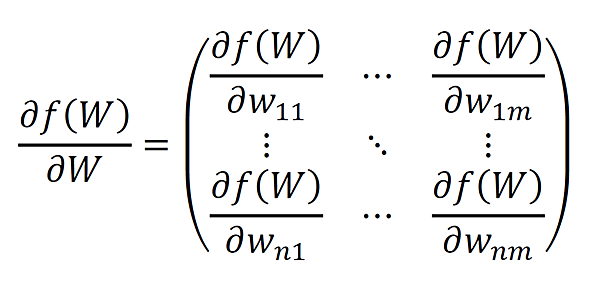目次
- はじめに
-
線形代数という武器
線形代数は線形空間及び線形変換と呼ばれる理論を中心に展開される非常に深い学問です。本気で説明しようとすると分厚い本になってしまいます。詳細は各書籍に譲るとして、ここでは機械学習の領域で頻出の以下の4つを学びましょう。
- スカラー・ベクトル・行列とは何か?
- 行列の和・積
- 行列の転置
- ベクトル・行列によるスカラーの微分
ポイント①:行列積は積をとる前の行列の「列」と後の行列の「列」のサイズが合っていないと計算できない。行列の転置 転置とは「行列の各要素を行番号と列番号をひっくり返した場所に移動すること」です。 例えば、 を転置すると、 になります。転置する前は1行2列目にあった2が、2列1行目に来ていますね。行列Aを転置したものをATと書きます。合わせて覚えましょう。 ベクトル・行列によるスカラーの微分 今回で一番重要なところです。第3回で学んだ「微分」の知識と、今回の「線形代数」の知識を融合して、機械学習で頻出の領域に一気に突入します。 さて復習になりますが、前回学んだ$\frac{ df }{ dx }$は「1つの値を返す関数fを、ある1つの変数xで微分する」という意味です。言い換えれば「スカラーを返す関数(スカラー関数と呼ぶ)をスカラーで微分する」ということになります。 今回はスカラーで微分する代わりにベクトルや行列で微分をしてみます。まったく難しくありません。ベクトル・行列はスカラーよりもサイズが大きいだけなのですから。 まず、「偏微分」という微分の親戚を理解しましょう。偏微分とは$\frac{ ∂f(x,y) }{ ∂x }$といったもののことです。通常の微分記号と違い、dが∂になっています。偏微分は「微分する変数以外を全て定数とみなして通常通り微分する」ということです。例えば、f(x,y)はxとyの二変数の関数になっていますが、x以外は全て定数(何かしらの数字)とみなして微分するということになります。 では、偏微分の知識をもとに、スカラーをベクトルで微分してみましょう。x,wをn次元縦ベクトル、f(x,w)はスカラー関数とします。このとき、f(x,w)をwで偏微分すると以下のようなn次元縦ベクトルができます。 ベクトルで微分すると、そのベクトルの要素1つ1つで偏微分をすることになるのですね! では、この勢いでスカラーを行列で微分してみましょう。Wをn×m行列、f(W)はスカラーを返す関数とします。このとき、f(W)をWで偏微分すると、下のようなn×m行列ができます。 こちらも、Wの要素1つ1つで偏微分すれば良いだけですね。 勾配降下法、再訪 ついに「すべての重みの更新式を統一的に表す」準備ができました。今回は下図を元に考えてみましょう。 誤差関数Eには一体何本の枝が関わっているでしょうか? まず1 つ目の出力y1にはw11,w12,…,w1mの合計m本の重みが関わっています。また2つ目の出力y2にもやはりw21,w22,…,w2mの合計m本の重みが関わっています。出力yは全部でn個あるので、誤差関数Eには合計mn個の重みが関わっていますね。 では、これらの重みをまとめて簡潔に表すにはどうしたら良いでしょうか? そうです、行列を使うのです。 1列目にはx1からの枝の重みが入っています。2列目、3列目以降も同様に各入力からの枝の重みが全て入っています。Wの1つで全ての重みを表現できています。この簡潔さが行列の強みです。 次に誤差関数について考えましょう。前回まではE(w)というように1つの重みだけを考えていましたが、今は全ての重みを考慮しているのでE(W)という表現が適切です。また誤差関数の傾き$\frac{ dE(w) }{ dw }$という表現も$\frac{ ∂E(W) }{ ∂W }$という行列による微分の表現に切り替えましょう。これも以下のように表すことができますね。 実は、これで全て終わりです。「すべての重みの更新式を統一的に表す」とは、スカラーで考えていたことをベクトルや行列を用いて多次元的に考えるだけなのです。重みの更新式も、前回までとほとんど変わらず以下のようになります。
ポイント②:積をとった後の行列のサイズに注意。k×m行列とm×n行列の積をとるとk×n行列になる。t 回目の全ての重みの更新式(勾配降下法)以前はスカラーだったwが行列Wに変わっただけですね! おわりに 線形代数の力を使って「全ての重みの更新を1つの数式で表す」ことができました。これは「微分」と「線形代数」という強力な武器のおかげです。機械学習の分野ではこの2つの武器はなくてはならないものなので、これをきっかけに復習してみると良いかもしれません。 次回はニューラルネットワークシリーズの締めくくりとして、誤差逆伝搬法(バックプロパゲーション)アルゴリズムをより具体的なモデルを元に説明していきます。以前学んだ「活性化関数」を覚えていますか? また新たなキーワードとして「連鎖律の原理」が登場します。お楽しみに!
w(t+1) ← w(t) ー ρ $\frac{ ∂E(W) }{ ∂W }$ (ρ > 0 ) - 勾配降下法、再訪
- おわりに
はじめに
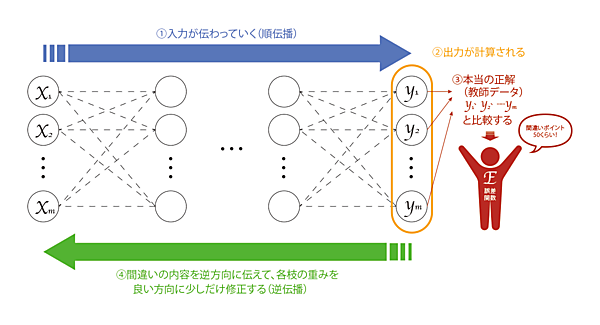
前回の第3回では、「逆伝搬」によるニューラルネットワークの学習について解説しました。「逆伝搬」は2つのStepの繰り返しでしたね(図1③④)。
まず、Step1ではニューラルネットワークが出力した予測値と実際の正解データを比較し、その間違いの度合いを「誤差関数E」によって計測します(図1③)。そしてStep2では、誤差関数の値が小さくなるようにネットワークの枝の重みwを更新するのでした(図1④)。
また、重みの更新ルールの説明では「勾配降下法」という非常に重要なアイデアが自然と導き出されることを紹介しました。
t 回目の重み更新式(勾配降下法)
w(t+1) ← w(t) ー ρ $\frac{ dE }{ dw }$ (ρ > 0 )
ニューラルネットワークの学習というプロセスは以上の内容に集約されています。「それでは、これで連載終了!お疲れさまでした!」と言いたいところですが、この更新式には1つだけ課題がありました。それは「1つの枝の重みwの更新しかできない」ことです。
ニューラルネットワークは文字通り「ネットワーク」であり、大量の枝が存在します。今回は「すべての重みの更新式を統一的に表す」ことを目標に解説していきます。そこで登場するのが「線形代数」と呼ばれる強力な武器です。
線形代数という武器
線形代数は線形空間及び線形変換と呼ばれる理論を中心に展開される非常に深い学問です。本気で説明しようとすると分厚い本になってしまいます。詳細は各書籍に譲るとして、ここでは機械学習の領域で頻出の以下の4つを学びましょう。
- スカラー・ベクトル・行列とは何か?
- 行列の和・積
- 行列の転置
- ベクトル・行列によるスカラーの微分
スカラー・ベクトル・行列とは何か?
スカラーとは1つの数字のこと。ベクトルと対比したときの数字をスカラーと言うのですが、とりあえず「1や2といったよく見る数字はスカラー!」程度で理解しておけば大丈夫です。
一方のベクトルは複数の数字を要素として括弧の中に並べたものです。プログラミング経験者には「配列」の方が分かりやすいかと思います。
このベクトルを縦ベクトルと呼びます。今回は要素が3つなので3次元縦ベクトルです。「縦」と言っているので「横」のベクトルもあるのですが、機械学習の分野では縦ベクトルで考えていくことがほとんどです。なお、ベクトルを表す変数は太字の斜体で表すことが多いです。
最後に行列です。行列も何のことはありません。数字を長方形に並べたものです。プログラミングの世界では「二次元配列」に相当するものです。
この場合は3行4列の行列もしくは3×4行列と呼びます。行列は斜体で表すことが多いです。ベクトルと行列を見比べると、ベクトルは列が1つの行列とみなすことができます。またスカラーも1×1行列とみなすことがあります。
行列の和・積
和とは足し算のことです。行列の和は非常に簡単です。同じ位置の要素同士を足すだけです。
とすると、和ABは以下のようになります。
同じ位置の要素同士を足すということは、和をとる2つの行列のサイズは同じでなければなりません。次の例では、2×3の2つの行列の和をとっています。
続いて行列の積です。積とは掛け算のこと。でも行列の積は少し変わった掛け算を行うので注意が必要です。
行列A,Bを
とすると、積ABは以下のようになります。
途端に複雑なことをしたように見えますが、結果の1つの要素に着目すればよく分かります。積の結果の1行1列目の値「a11 b11 + a12 b21 + … + a1m bm1」を見て、これがどこから出てきたのか推測してみましょう。
正解は「Aの1行目とBの1列目を取り出して中の要素ごとに積をとったもの」です。言葉で聞くと意外と単純なことをしていますね。ABの結果のi行j列目は「Aのi行目とBのj列目を取り出して中の要素ごとに積をとったもの」というようにルール化できます。
具体的な行列を使って計算してみると、以下のようになります。
行列の積は以下の2つのポイントを知っておくと、間違いを防ぐことができます。
ポイント①:行列積は積をとる前の行列の「列」と後の行列の「列」のサイズが合っていないと計算できない。
ポイント②:積をとった後の行列のサイズに注意。k×m行列とm×n行列の積をとるとk×n行列になる。
行列の転置
転置とは「行列の各要素を行番号と列番号をひっくり返した場所に移動すること」です。
例えば、
を転置すると、
になります。転置する前は1行2列目にあった2が、2列1行目に来ていますね。行列Aを転置したものをATと書きます。合わせて覚えましょう。
ベクトル・行列によるスカラーの微分
今回で一番重要なところです。第3回で学んだ「微分」の知識と、今回の「線形代数」の知識を融合して、機械学習で頻出の領域に一気に突入します。
さて復習になりますが、前回学んだ$\frac{ df }{ dx }$は「1つの値を返す関数fを、ある1つの変数xで微分する」という意味です。言い換えれば「スカラーを返す関数(スカラー関数と呼ぶ)をスカラーで微分する」ということになります。
今回はスカラーで微分する代わりにベクトルや行列で微分をしてみます。まったく難しくありません。ベクトル・行列はスカラーよりもサイズが大きいだけなのですから。
まず、「偏微分」という微分の親戚を理解しましょう。偏微分とは$\frac{ ∂f(x,y) }{ ∂x }$といったもののことです。通常の微分記号と違い、dが∂になっています。偏微分は「微分する変数以外を全て定数とみなして通常通り微分する」ということです。例えば、f(x,y)はxとyの二変数の関数になっていますが、x以外は全て定数(何かしらの数字)とみなして微分するということになります。
では、偏微分の知識をもとに、スカラーをベクトルで微分してみましょう。x,wをn次元縦ベクトル、f(x,w)はスカラー関数とします。このとき、f(x,w)をwで偏微分すると以下のようなn次元縦ベクトルができます。
ベクトルで微分すると、そのベクトルの要素1つ1つで偏微分をすることになるのですね!
では、この勢いでスカラーを行列で微分してみましょう。Wをn×m行列、f(W)はスカラーを返す関数とします。このとき、f(W)をWで偏微分すると、下のようなn×m行列ができます。
こちらも、Wの要素1つ1つで偏微分すれば良いだけですね。
勾配降下法、再訪
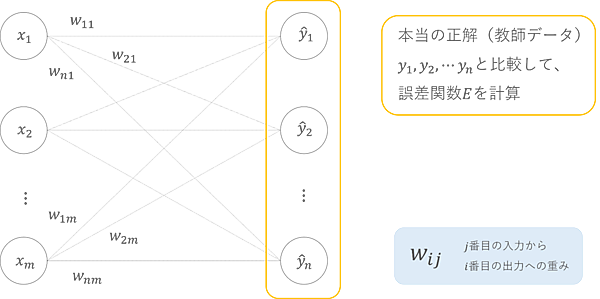
ついに「すべての重みの更新式を統一的に表す」準備ができました。今回は下図を元に考えてみましょう。
誤差関数Eには一体何本の枝が関わっているでしょうか? まず1 つ目の出力y1にはw11,w12,…,w1mの合計m本の重みが関わっています。また2つ目の出力y2にもやはりw21,w22,…,w2mの合計m本の重みが関わっています。出力yは全部でn個あるので、誤差関数Eには合計mn個の重みが関わっていますね。
では、これらの重みをまとめて簡潔に表すにはどうしたら良いでしょうか? そうです、行列を使うのです。
1列目にはx1からの枝の重みが入っています。2列目、3列目以降も同様に各入力からの枝の重みが全て入っています。Wの1つで全ての重みを表現できています。この簡潔さが行列の強みです。
次に誤差関数について考えましょう。前回まではE(w)というように1つの重みだけを考えていましたが、今は全ての重みを考慮しているのでE(W)という表現が適切です。また誤差関数の傾き$\frac{ dE(w) }{ dw }$という表現も$\frac{ ∂E(W) }{ ∂W }$という行列による微分の表現に切り替えましょう。これも以下のように表すことができますね。
実は、これで全て終わりです。「すべての重みの更新式を統一的に表す」とは、スカラーで考えていたことをベクトルや行列を用いて多次元的に考えるだけなのです。重みの更新式も、前回までとほとんど変わらず以下のようになります。
t 回目の全ての重みの更新式(勾配降下法)
w(t+1) ← w(t) ー ρ $\frac{ ∂E(W) }{ ∂W }$ (ρ > 0 )
以前はスカラーだったwが行列Wに変わっただけですね!
おわりに
線形代数の力を使って「全ての重みの更新を1つの数式で表す」ことができました。これは「微分」と「線形代数」という強力な武器のおかげです。機械学習の分野ではこの2つの武器はなくてはならないものなので、これをきっかけに復習してみると良いかもしれません。
次回はニューラルネットワークシリーズの締めくくりとして、誤差逆伝搬法(バックプロパゲーション)アルゴリズムをより具体的なモデルを元に説明していきます。以前学んだ「活性化関数」を覚えていますか? また新たなキーワードとして「連鎖律の原理」が登場します。お楽しみに!