はじめに
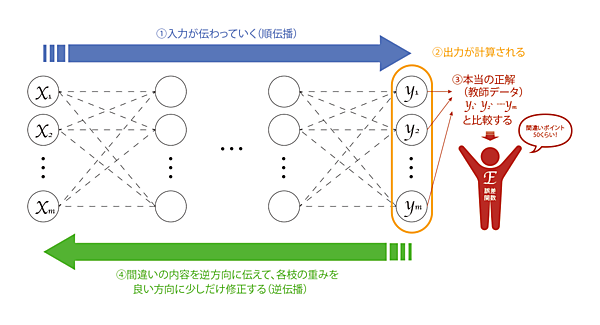
前回は、ニューラルネットワークの「順伝播」について詳細な計算の仕組みを解説しました。具体的には、順伝播の計算は「1次関数」→「活性化関数」の繰り返しによって行われ、これにより入力がニューラルネットワークを伝わりながら計算されて出力値の予測値が吐き出されるというわけです(下図①②)。
さて、予測を正しく行うためには、逆伝播によりニューラルネットワークが「学習」をしなければなりません(下図③④)。具体的には、
逆伝播のStep1.
②による出力(予測値)と実際の正解(教師データ)を比較。その間違いの度合を「誤差関数E」によって計測する
逆伝播のStep2.
誤差関数Eの値が小さくなるように、各枝の重みを更新する
これを繰り返すのが、逆伝播のざっくりとした流れです。
誤差関数Eとは
「誤差関数E」とは、出力(予測値)と実際の正解が「どのくらいズレているのか」をうまく計算してくれるように作った関数のことです。例えば、二乗誤差の総和
$$E = \frac{ 1 }{ 2 } \sum_{ i } \Biggl( y^i - y_i \Biggr) ^2$$
などが使われます(今はこの式の意味が分からなくても大丈夫です)。誤差関数は、いわば「間違いカウンター」のような関数です。出力(予測値)と実際の正解が近ければ誤差関数Eの値は小さく、遠ければ誤差関数Eの値は大きくなります。ということは、この誤差関数Eの値が小さくなるようにニューラルネットワークの各枝の重みを更新して行けば、「間違いが少ない」出力予測ができるニューラルネットワークが出来上がるのではないか?という気持ちになります。これこそがニューラルネットワークの学習なのです。
微分の定義
さて、この学習を行うアイデアを理解するために、非常に強力な「微分」という数学の武器を導入します。もしかしたら、高校や大学で習った記憶がある方も多いのではないでしょうか。でも、数学って使わないと忘れてしまいますよね。ここで微分について復習しておきましょう。
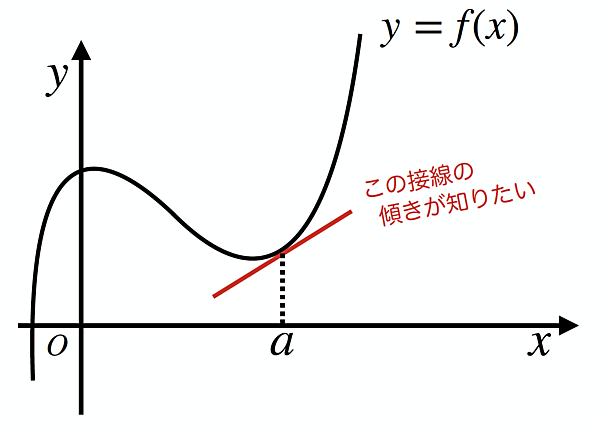
ある関数y=f(x) の、とある点x=aでの接線の傾きを求める流れを考えてみます(下図)。
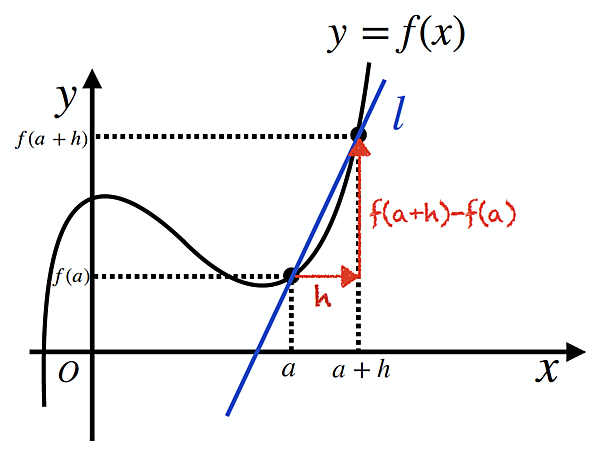
いきなり接線の傾きを求めるのは難しいので、一旦、x=aのところからhだけ離れたx=a+hを考えて、関数上の2点を結んでできる直線lを考えます(下図)。
すると、この直線の傾きは
$$\frac{ f(a)-f(a + h) }{ h }$$
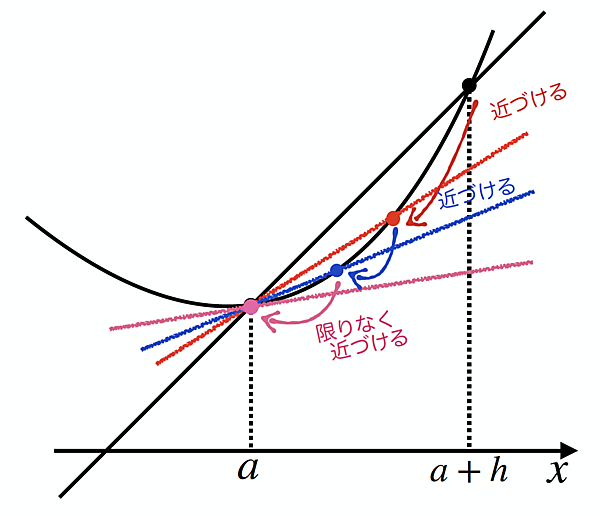
で表せることが分かります。実は、これでx=aにおける接線の傾きまで目の前です。というのも、次図のようにhを0に限りなく近づけると、直線lは限りなく「x=aにおける接線」に近づいて行きますよね。
というわけで、「hを限りなく0に近づける」という意味の記号$\lim_{h \to 0}$をくっつけます。
$$\lim_{h \to 0} \frac{ f(a + h )-f( a ) }{ h } \\$$
これは、まぎれもなく「関数y=f(x)のx=aにおける接線の傾き」に相当することが分かります。この値をf’(a)と表し、y=f(x)のx=aにおける「微分係数」と呼びます。
微分係数の定義
以下のように定義される f' (a) を、関数 y=f(x) の x=a における微分係数と呼ぶ。
$$f'( a ) = \lim_{h \to 0} \frac{ f(a + h)-f( a ) }{ h } \\$$
f' (a) は「関数 y=f(x) の x=a における接線の傾き」のことである。
そして、x=a というようにいちいち1つの点を決めうちにするのも面倒なので、いっそ x の関数として「xに値を代入するとその点での接線の傾きが計算される関数」を作れば便利なのではないかという考えに至ります。これを f' (x) と書き、y=f(x) の「導関数」と呼びます。
導関数の定義
以下のように定義される関数 f' (x) を、関数 y=f(x) の導関数と呼ぶ。
$$f'( x ) = \lim_{h \to 0} \frac{ f(x + h)-f( x ) }{ h } \\$$
f' (x) は「各xに対し、その点での接線の傾きを返す」ような関数のことである。
ここで、y=f(x) の導関数 f' (x) を計算することを「y=f(x) を微分する」と呼ぶことにしましょう。ちなみに、導関数 f' (x) は$\frac{ df }{ dx }$と表すことも多いです。むしろ、機械学習ではこちらの書き方のほうが多いかも。
何が嬉しい?「微分」の威力
ところで、微分を知っていると一体何が嬉しいのでしょうか。思い出してください。我々の目標は「誤差関数 E の値が小さくなる」ように重みwを更新して行くことでした。
実は、微分を使えばこのアイデアを実現できてしまうのです。その「超重要」なアイデアをざっくりと説明しましょう。
今、関数 E(w) を考えます。この関数の形が、下図のように単純なものだったとしましょう。
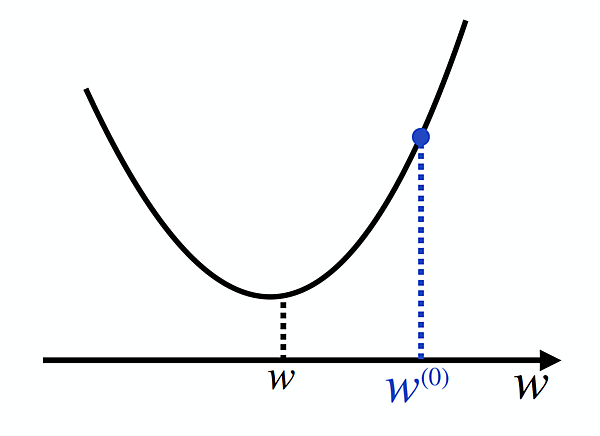
目標は、この関数 E(w) が一番小さくなるようなwを見つけることです。すなわち、下図のwの場所を見つけることです。そのために、まずは適当なwの初期値w(0)を設定しましょう(右肩の(0)は「更新回数0回目」であることを意味しています)。
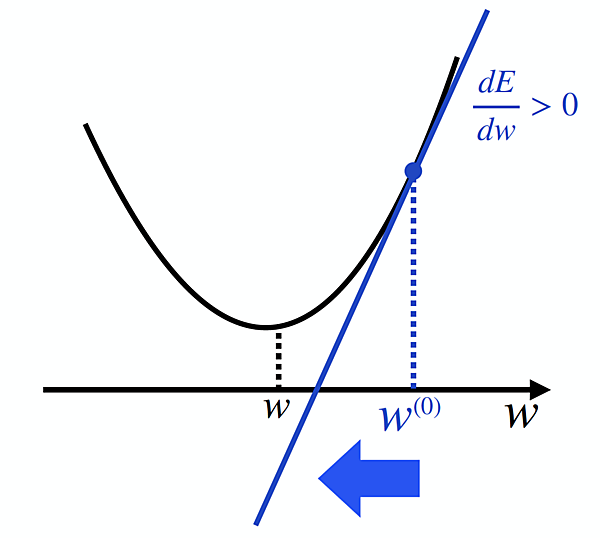
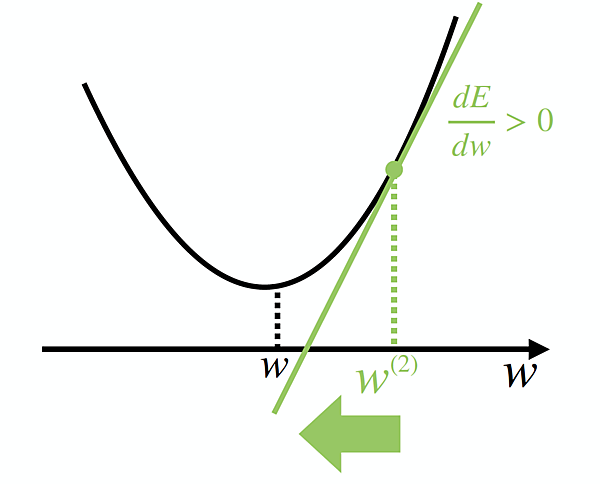
さて、ここで微分の出番です。E(w)の導関数 $\frac{ dE }{ dw }$ の値を計算してみるのです。これは「w=w_0 における接線の傾き」を表すのでした。ということは、下図のように $\frac{ dE }{ dw }$ > 0 となることが分かるでしょう。
接線の傾き>0 ということは、関数の形を参考にすれば、wをw0より負の方向に動かせば良いことがわかります。すなわち、wを $\frac{ dE }{ dw }$ の逆方向に動かすことを繰り返せば良さそうだ!ということが分かるのです。よって更新後のw(1)は、なんとなくw(1) ← w(0) ー $\frac{ dE }{ dw }$と計算するのが良さそうです。
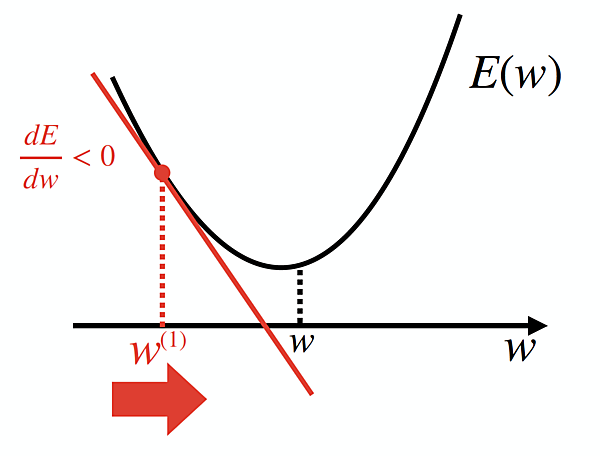
これにより、今度はw(1)が下図のように更新されたとします。
すると、今度は $\frac{ dE }{ dw }$ < 0 となり、w(2)は w(1) よりも $\frac{ dE }{ dw }$ の逆方向に動かせば良いので、w(2) ← w(1) ー $\frac{ dE }{ dw }$となります。これにより、今度は w(2)が下図のようになり……といったようにwの値を更新して行けば良さそうですね。
しかし、何も考えずに $\frac{ dE }{ dw }$ をそのまま引いて更新し続けるだけでは、$\frac{ dE }{ dw }$ の大きさによっては求めたいwがいつまでも見つからなかったり、場合によってはどこか遠くに発散してしまったりするかもしれません。そこで、適切な小さな正の数pを設定し、それを $\frac{ dE }{ dw }$ にかけてから引くことで「値を大きくずらしすぎる」ことを防ぎます(このpを「学習率」と呼びます)。
以上をまとめると、重みの更新ルールは以下のように書けば良さそうです。
t 回目の重み更新式(勾配降下法)
w(t+1) ← w(t) ー ρ $\frac{ dE }{ dw }$ (ρ > 0 )
実は、これが「勾配降下法(GD)」のアイデアそのものなのです。実際はもう少し複雑な形の式になりますが、基本アイデアはこれで尽くされています。要するに「微分の値を手がかりに、少しずつ谷底に近づいていく」のが、ニューラルネットワークの学習そのものなのです。
どうやら、微分とはずいぶんと長い付き合いになりそうですね。実際に、微分はあらゆるところで我々を助けてくれる凄まじい威力を持つ概念ですので、ぜひ皆さんも今から微分と仲良くなっておいてくださいね。
実は、全ての枝の重みは、このルールに従って更新することになります。ところが、現段階で得られている式では、「1つの枝の重み」しか扱うことができません。
そこで、次回以降は「線形代数」という武器を使って「すべての重みの更新式」を統一的にビシッと表すことを目標に解説していきたいと思います。
- この記事のキーワード