負の値は必要? 解釈しやすい行列分解「NMF」

はじめに

「できないよりは、できた方が良いよね」と言った後に(いや。できないからこそ見える世界もあるな…)と思ったことを今でも忘れられない。

それはさておき。基本的に科学はできることを増やすためにある。医学は治せる病気の数を増やすためにあり、数学は科学の共通言語としてなんでも語れるようにするためにある(と思っている)。0の概念を発見し、負の数を作り、ついには虚数を編み出したりしながら、あの手この手で数学はその世界を拡大してきたように思う。

おかげで確かにできることは増えたが、虚数はまだしも、負の数がないと実社会は上手く機能しない。ところが、ここで「負の数なんて知らないよ」というデータ分析手法が現れる。「そんな手法が本当に役に立つの?」と少し疑いながらその気持ちを探ってみると、データと向き合う姿勢が少し改まる。

非負値行列因子分解とは一体何者?

今回は、負の数を扱えない「非負値行列因子分解」という分析手法を学びましょう。

非負値行列因子分解は通称NMFと呼ばれます。これはNon-negative Matrix Factorizationの略です。Non-negativeは「非負」、つまり負の値ではないこと、Matrixは「行列」を意味します。Factorizationは直訳をすると因数分解です。因数分解とはなんだか懐かしい響きですが、例えば$x^2 + 7x + 12$を$(x + 4)(x + 3)$ といった「積の表現」に書き換えることですね。

まとめると、NMFとは、

ということになります。数式で表すと、分解前の行列を$V$としたときには、

となるような非負値行列$W$と$H$を発見することに相当します。≅は「およそ等しい」という意味の記号です。ぴったり同じような$WH$を求めることはとても難しいので、そのような表現を使っています(今回は解説しませんが、この$W$と$H$は最適化の手法を用いて求めます)。

「負の数を扱えない」の気持ち：
顔の特徴を抽出してみよう

1つの行列を非負値の行列に分解するとは一体どういうことでしょうか。そしてそれが何に応用されているのでしょうか。今回は、この2つの謎を追っていくことにしましょう。まずは具体例を用いてNMFの分解の“気持ち”を理解していきます。「非負に分解する」ことは実はすごい効果を持っているのです!

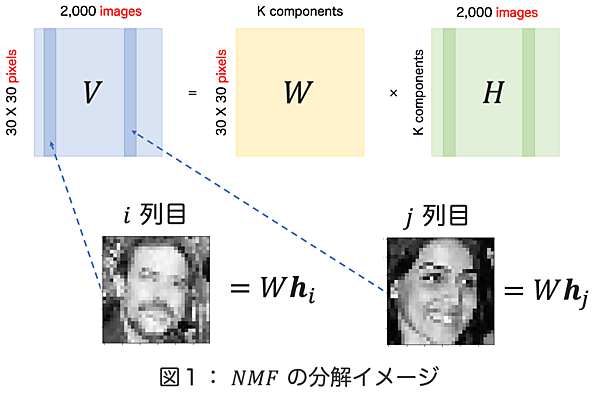
今回は分解したい行列$V$の各列に一次元に引き伸ばした画像を入れておきます。この画像は顔認識で用いられるデータセットに前処理を加えたものです(データセット：VGG Face2; Creative Commons Attribution-ShareAlike 4.0 International License)。$V$の行と列がそれぞれ画素数と画像の枚数に対応することになりますね。では、図1のように、この行列$V$を$W$と$H$という2つの行列に分解していきましょう。行列の積の性質から、行列$V$の$i$列目に格納された画像は、行列$W$と行列$H$のi列目を用いて表現できることが分かりますか。

着目すべきは行列$W$が画像$i$と画像$j$で共通になるということです。これを解釈すると「NMFは画像の集まりである行列$V$の中に潜む共通の特徴$W$を取り出すことができる」と考えられないでしょうか。今、行列$V$は顔の画像で構成されています。「複数の顔写真の共通の特徴」と言われて何を思い浮かべますか。色々と考えられると思いますが、例えば、鼻、口、目といった顔のパーツは共通の特徴と言えるかもしれませんね。

それでは実験してみましょう。Python機械学習ライブラリsckikit-learnを使えば、NMFはほんの数行で実行できます。ぜひ試してみてください。なお、分解後の行列$W$の列数および行列$H$の行数に当たる$K$は分析者が設定するハイパーパラメータとなります。この$K$の設定が分析者を悩ますところですが、行列$V$の行数と列数の調和平均の値を参考にしたり、$V$と$WH$の近似誤差を見ながら上手く設定していくのが一般的です(今回は$K = 90$としました）。図2が実験結果です。

どうでしょうか。顔全体をぼんやり表すような特徴も入っていますが、顔の部分的なパーツを抽出しているようなものもありませんか。$V$の$i$番目の画像に着目すると$v_i = Wh_i$という関係式が成り立つので、各画像に対して図3のような結果が得られます。

少しぼやけていますが、うまく特徴を掴んで顔を再構成できているように見えますね。ここで改めて強調しておくと、$W$の値は共通で、$h_i$の中身がオリジナル画像$V_i$ごとに異なります。$W$の中に入っている顔の特徴を組み合わせて($W$に$h_i$を掛けて)、オリジナル画像を再構成しているということです。

これまでの結果を元に「NMFは顔の特徴を抽出できる! 何だかすごいぞ!」と終わってしまうのはもったいないですね。もう一歩進んで「なぜ顔の特徴をパーツ単位で捉えることができたのか」という疑問を考えていきましょう。

普段、私たちはどのように顔の絵を描いているでしょうか。おそらく殆どの方が、輪郭を描いた後に目・口・鼻などのパーツを書き加えていくのではないでしょうか。この「書き加える」ことが非常に重要です。

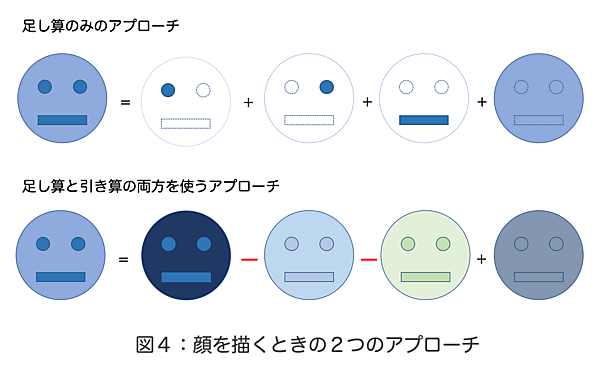
「書き加える」ということは、数学の計算で表現すると「足し算をする」ことに他なりません。図4は同じ顔の絵を描こうとしています。「足し算のみのアプローチ」と「足し算と引き算の両方を使うアプローチ」がありますが、最終的には同じ顔を得ることができます。引き算も可能ということは「書き足す」だけでなく「書き減らす」こともできるので、人間ワザではない不思議なアプローチで顔を描くことができますね。

これでNMFの気持ちが分かりました。Non-negativeをひと言で表すと「足し算的にデータを見るよ」ということですね。

NMFの応用先

最後にNMFの応用例を見ていきましょう。まずは行列$W$に着目した応用例から。NMFに課せられた「非負値」という制約により、行列$W$には解釈しやすい特徴が出現する可能性があります。これに着目して、例えば医学・生理学分野では細胞の自動検出に応用されています。動画形式の細胞の活動データを$V$に格納して$W$に細胞の位置の情報を集約させる試みです。数えきれない程大量にある細胞が行列$W$の各列に少しずつばらけてくれれば、細胞の観察がしやすそうですね。

行列$H$に着目した応用例もあります。行列$W$とは異なり行列$H$は行列$V$の「列ごとに」求められます。$v_i = Wh_i$という関係性のことですね。これは、見方を変えると$h_i$が$v_i$の”id”のような役割を果たすと考えられます。これは何に使えそうでしょうか。

例えば、今回の例では$h_i$が顔画像に対応したidだと解釈すれば顔認識に使えそうですね。また、顧客分析にも活用できます。顧客データを分解して得られた$h_i$を用いて教師なしのクラスタリングを行うのです。$h_i$は$K$次元のベクトルですが、$h_i$のうち最も大きな値を持つ要素の位置をそのままクラスター番号に割り当てると、顧客をK個のクラスターに分割できます。

この他にも、NMFは教師あり学習の枠組みにも拡張でき、例えば音源分離に活用されています。NMFの応用先が多岐に渡る理由は、分解後の行列が解釈しやすいこと、そしてNMFがシンプルな構造を持っていることが挙げられます。アイデア1つで様々なことに応用できますね。

おわりに

実社会では負の値が必要不可欠です。例えば赤字・黒字という概念は正・負という概念がなければ成り立ちません。しかし、それとは別に「正の値しか取らない」というデータも沢山あるというのも事実です。画像がその代表格ですね。「負の値なんて知らないよ」というNMFは、ある意味で負の値を取らないデータと誠実に向き合っていると言えるかもしれません。

次回は、今回登場したNMFに隠されたもう1つの性質を見ていきたいと思います。その名も「スパース」。聞き慣れない横文字が出てきましたが、NMFに限らずこの性質がデータ解析では非常に重要となってくるのです。次回もお楽しみに!