幾何学模様を作成する
幾何学模様を作成する
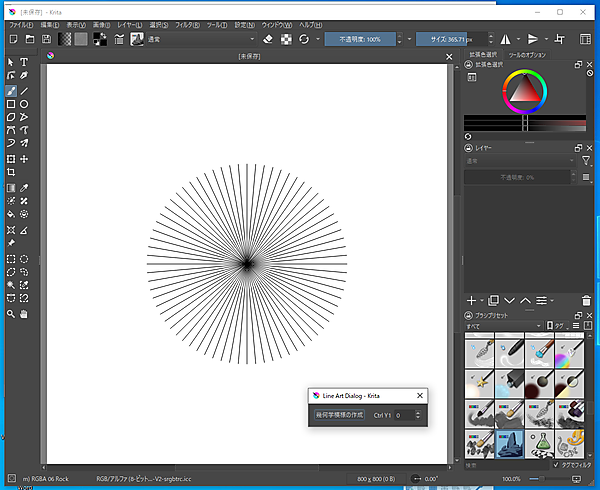
まず、プッシュボタンUIで直線を回転させながら複製すると単純な放射状の幾何学模様が作れます。さらにスピンボックスUIで1つ目のコントロールポイントのY座標を移動してプッシュボタンUIを押すと、ちょっとした幾何学模様が作れます。それから2つのコントロールポイントのXY座標を移動できるようにすれば本格的な幾何学模様が作れます。
プッシュボタンUIを押して幾何学模様を描画
サンプルスクリプト「dlg_bezier2.py」に追加して、次のスクリプトを追記します。スピンボックスUIを操作するときはベジェ曲線1本だけを描画し、プッシュボタンUIを押したときに放射状にベジェ曲線を回転させて描画します(図5)。ベジェ曲線のコントロールポイントは第5回で解説した通り、直線を磁石で引っ張ったような座標です。
・サンプルスクリプト「dlg_bezier3.py」# モジュール
from PyQt5.Qt import *
from PyQt5.QtWidgets import QDialog, QHBoxLayout, QSpinBox, QLabel, QPushButton
from krita import *
# ダイアログクラス
class Dialog(QDialog):
(中略)
# ベジェ曲線の描画
def bezier(self,painter):
path = QPainterPath()
ctrl_x1 = 100
ctrl_y1 = self.sb_ctrl_y1.value()
ctrl_x2 = 200
ctrl_y2 = 0
path.cubicTo(ctrl_x1,ctrl_y1,ctrl_x2,ctrl_y2,200,0)
painter.drawPath(path)
# ボタンが押されたら幾何学模様の描画
def click_button(self):
self.img = self.draw_bezier(360)
self.set_layer()
self.doc.refreshProjection()
(中略)
# メイン処理
def create(self):
self.create_doc(800,800)
layout = QHBoxLayout()
self.button = QPushButton("幾何学模様の作成")
layout.addWidget(self.button)
self.button.clicked.connect(self.click_button)
# QLabel Ctrl Y1
self.label_ctrl_y1 = QLabel(" Ctrl Y1")
layout.addWidget(self.label_ctrl_y1)
# QSpinBox Ctrl Y1
self.sb_ctrl_y1 = QSpinBox()
self.sb_ctrl_y1.setMinimum(-2000)
self.sb_ctrl_y1.setMaximum(2000)
self.sb_ctrl_y1.setSingleStep(50)
self.sb_ctrl_y1.valueChanged.connect(self.click_sb)
layout.addWidget(self.sb_ctrl_y1)
self.setLayout(layout)
# 最初の直線の描画
self.click_sb()
(後略)【サンプルスクリプトの解説】
PyQt5モジュールのスピンボックスUIとラベルUIとプッシュボタンUIのウィジェットを読み込みます。
bezierメソッドでベジェ曲線の1つ目のコントロールポイントのY座標だけ移動を反映します。
「click_button」メソッドでプッシュボタンUIが押されたら360度の放射状に回転させたベジェ曲線を描きます。
createメソッドでプッシュボタンUIとスピンボックスUIを配置します。1つ目のコントロールポイントのY座標が変化したらclick_sbメソッドを呼び出すようにフックします。
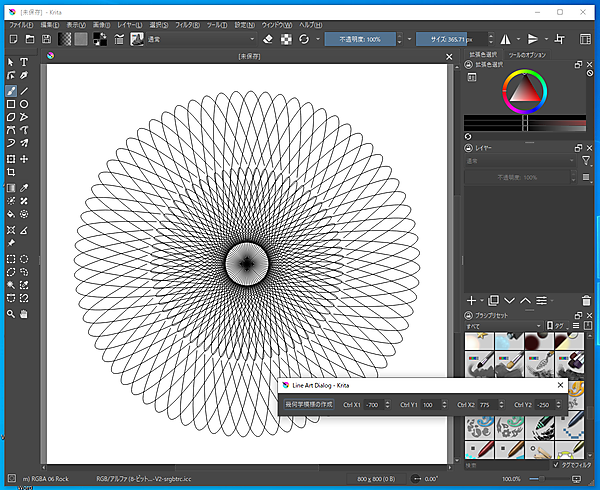
ベジェ曲線の変形を仕上げる
サンプルスクリプト「dlg_bezier3.py」に追加して、次のスクリプトを追記します。ベジェ曲線の2つのコントロールポイントのXY座標も移動できるようにしました(図5)。これで完成です。つまり幾何学模様は1つの図形を規則的に繰り返しているだけなんですね。
・サンプルスクリプト「dlg_bezier4.py」(前略)
# ダイアログクラス
class Dialog(QDialog):
(中略)
# ベジェ曲線の描画
def bezier(self,painter):
path = QPainterPath()
ctrl_x1 = self.sb_ctrl_x1.value()
ctrl_y1 = self.sb_ctrl_y1.value()
ctrl_x2 = self.sb_ctrl_x2.value()
ctrl_y2 = self.sb_ctrl_y2.value()
path.cubicTo(ctrl_x1,ctrl_y1,ctrl_x2,ctrl_y2,200,0)
painter.drawPath(path)
(中略)
# メイン処理
def create(self):
self.create_doc(800,800)
layout = QHBoxLayout()
self.button = QPushButton("幾何学模様の作成")
layout.addWidget(self.button)
self.button.clicked.connect(self.click_button)
# QLabel Ctrl X1
self.label_x1 = QLabel(" Ctrl X1")
layout.addWidget(self.label_x1)
# QSpinBox Ctrl X1
self.sb_ctrl_x1 = QSpinBox()
self.sb_ctrl_x1.setMinimum(-1000)
self.sb_ctrl_x1.setMaximum(1000)
self.sb_ctrl_x1.setSingleStep(25)
self.sb_ctrl_x1.setValue(50)
self.sb_ctrl_x1.valueChanged.connect(self.click_sb)
layout.addWidget(self.sb_ctrl_x1)
# QLabel Ctrl Y1
self.label_ctrl_y1 = QLabel(" Ctrl Y1")
layout.addWidget(self.label_ctrl_y1)
# QSpinBox Ctrl Y1
self.sb_ctrl_y1 = QSpinBox()
self.sb_ctrl_y1.setMinimum(-2000)
self.sb_ctrl_y1.setMaximum(2000)
self.sb_ctrl_y1.setSingleStep(50)
self.sb_ctrl_y1.valueChanged.connect(self.click_sb)
layout.addWidget(self.sb_ctrl_y1)
# QLabel Ctrl X2
self.label_x2 = QLabel(" Ctrl X2")
layout.addWidget(self.label_x2)
# QSpinBox Ctrl X2
self.sb_ctrl_x2 = QSpinBox()
self.sb_ctrl_x2.setMinimum(-1000)
self.sb_ctrl_x2.setMaximum(1000)
self.sb_ctrl_x2.setSingleStep(25)
self.sb_ctrl_x2.setValue(150)
self.sb_ctrl_x2.valueChanged.connect(self.click_sb)
layout.addWidget(self.sb_ctrl_x2)
# QLabel Ctrl Y2
self.label_ctrl_y2 = QLabel(" Ctrl Y2")
layout.addWidget(self.label_ctrl_y2)
# QSpinBox Ctrl Y2
self.sb_ctrl_y2 = QSpinBox()
self.sb_ctrl_y2.setMinimum(-2000)
self.sb_ctrl_y2.setMaximum(2000)
self.sb_ctrl_y2.setSingleStep(50)
self.sb_ctrl_y2.valueChanged.connect(self.click_sb)
layout.addWidget(self.sb_ctrl_y2)
self.setLayout(layout)
# 最初の直線の描画
self.click_sb()
(後略)【サンプルスクリプトの解説】
bezierメソッドで2つのコントロールポイントのXY座標の移動を反映します。
createメソッドで2つのコントロールポイントのXY座標のスピンボックスUIを配置し、click_sbメソッドにフックします。1つ目のコントロールポイントのスピンボックスUIがsb_ctrl_x1プロパティとsb_ctrl_y1プロパティで、2つ目のコントロールポイントのスピンボックスUIがsb_ctrl_x2プロパティとsb_ctrl_y2プロパティです。