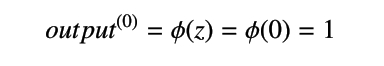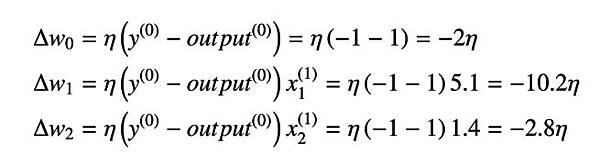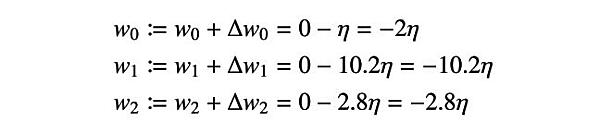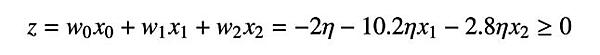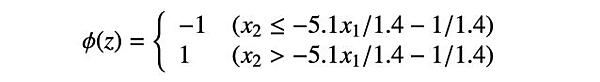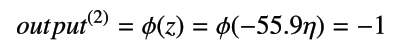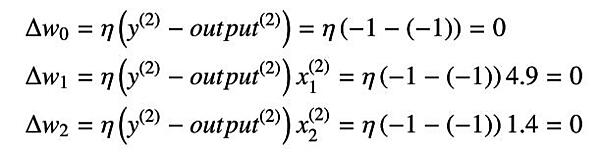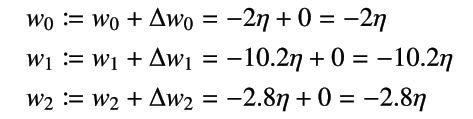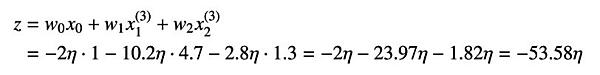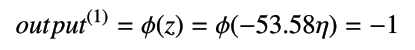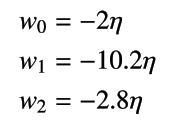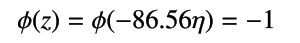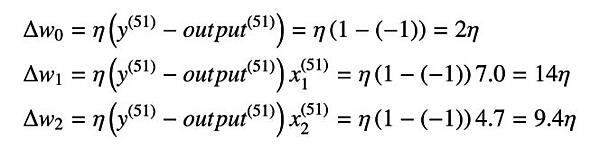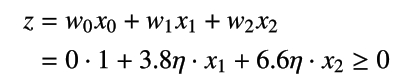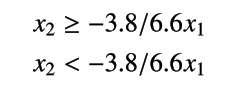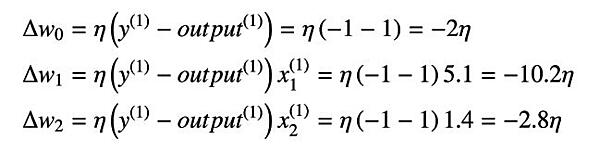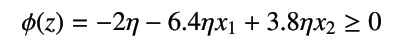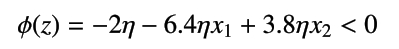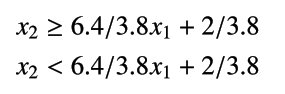具体例で数式を読み解く

具体例で数式を読み解く

ここからは具体例を考えてみましょう。ここでは、入力信号は2 つあるとします。すなわち、入力信号x₁、x₂ に対して総入力z を

総入力z = w0x0 + w1x1 + w2x2

とします。ここで、重みw₀、w₁、w₂ をそれぞれ0 で初期化します。すなわち、以下のように設定します。

w0 = 0, w1 = 0, w2 = 0

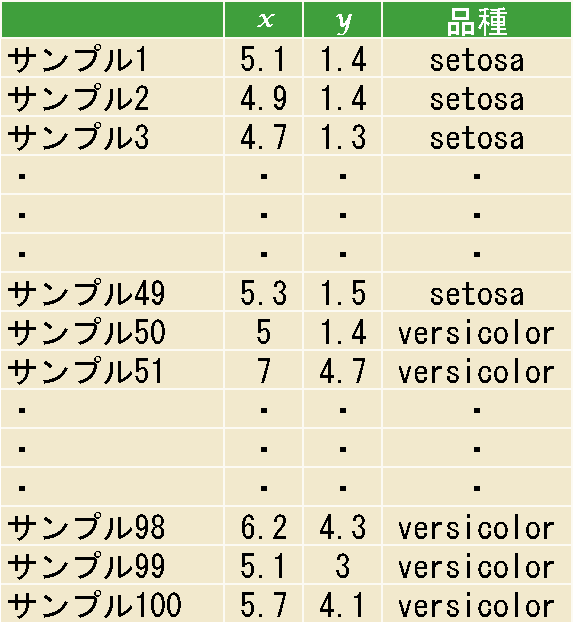
ここでは、2.3 節「Iris データセットでのパーセプトロンモデルのトレーニング」で扱われるIris データセットの品種がsetosa, versicolor のデータを抽出してみます。

1 番目から50 番目までのサンプルの品種はsetosa、51 番目から100 番目までのサンプルの品種がversicolorです。

1 番目のサンプルは、x₁⁽¹⁾ = 5.1、x₂⁽¹⁾ = 1.4、y⁽¹⁾ = -1 です。したがって、総入力z は以下のようになります。

z = w₀x₀ + w₁x₁⁽¹⁾ + w₂x₂⁽¹⁾ = 0・1 + 0・5.1 + 0・1.4 = 0

活性化関数の出力は、次のようになります。

以上により、1 番目のサンプルの品種は setosa であり y⁽⁰⁾ = -1 であるにもかかわらず、予測結果はŷ⁽⁰⁾ = 1 となったことを確認できます。このとき、重みの更新量は、以下のようになります。

そのため、重み w₀、w₁、w₂ は次のように更新されます。

以上により、総入力 z が

ならば setosa 、そうでないならば versicolorと判定します。したがって、

以上の結果得られる決定境界 (この場合は品種を識別する境界線) を図2に示します。

図2： 1 番目のサンプルを用いて重みを更新した後の決定境界

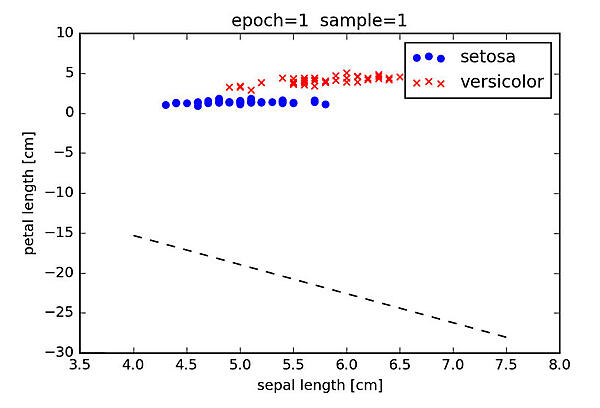
2 番目のサンプルは、x₁⁽²⁾ = 4.9、x₂⁽²⁾ = 1.4、y⁽²⁾ = -1 です。したがって、総入力は以下のようになります。

となります。したがって、出力信号は

となります。よって、重みの更新量は以下のようになります。

したがって、重みは以下のように更新されます。

2 番目のサンプルを用いると重みの値は更新されないことを確認できます。3 番目のサンプルはx₁⁽³⁾ = 4.7、x₂⁽³⁾ = 1.3、y⁽³⁾ = -1 です。したがって、

となります。したがって、出力信号は

となります。重みの更新量は、以下のようになります。

以上のようにして、2 番目から 50 番目までのサンプルでは重みは更新されません。したがって、50 番目のサンプルが終了した時点での重みは、

となります。

続いて、51 番目のサンプルはx₁⁽⁵¹⁾ = 7.0、x₂⁽⁵¹⁾ = 4.7、y⁽⁵¹⁾ = 1 となります。 総入力 z⁽⁵¹⁾は、以下のようになります。

したがって、

となります。重みの更新量は以下のようになります。

重みは以下のように更新されます。

以上により、

このときは品種が versicolor、そうではないときは品種が setosa と判定されることを確認できます。以上を整理すると、

以上の状況を可視化すると、図3を得ます。

図3： 51 番目のサンプルを用いて重みを更新した後の判別境界

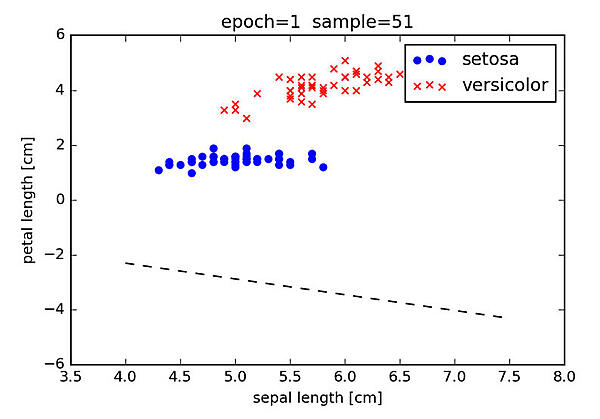
52 番目から 100 番目のサンプルでは重みの更新が行われません。

続いて、2 巡目に入っていきます。1 番目のサンプルは、x₁⁽¹⁾ = 5.1、x₂⁽¹⁾ = 1.4、y⁽¹⁾ = -1 です。したがって、総入力zは以下のようになります。

となります。よって、

となります。重みの更新量は、

となります。したがって、

以上の結果、総入力 z は、以下のように表されます。

したがって、活性化関数が

のときは 1 を、

のときは -1 となります。

以上を整理すると、

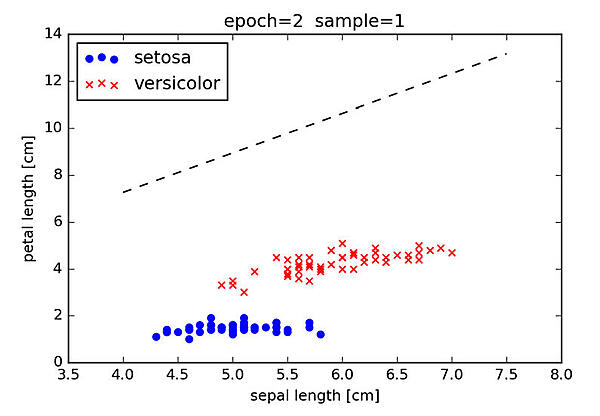
となります。この状況を可視化すると、図4のようになります。判別境界の直線が右肩上がりになり、さらにすべての点はこの直線よりも下側にあること (つまり、この判別境界を用いるとすべてが setosa と判定される) を確認できます。

図4：1 番目のサンプルを用いて重みを更新した後の決定境界