「複雑」をたくさんの「単純」に分解する〜順伝播は「1次関数」と「単純な非線形」の繰り返し

「電気信号が脳を伝わっていく流れを再現する」という直感的かつ身近な例による説明に「ピンとくる」という人も、きっと多いのだと思います。でも、筆者は何だかこの説明にいまいち「ピンとこない」時期が続いたのを覚えています。「わかりやすい説明」は人によって違うものだと思いますし、おそらく、筆者と同じ悩みを抱えている方も一定数いらっしゃるのではないでしょうか。

そこで今回は、一旦「脳の神経細胞」のことは忘れて、同じことの「数学的」アプローチによる理解を試みてみましょう。

前回で、我々にとっての目標は「関数の近似」であることを説明しました。そして、一般的に世の中に溢れかえっている「関数」は、ものすごく複雑な様相をしているのが普通なのだということにも触れました。

簡単な関数と難しい関数

x₁,x₂,…,x_Nの関数 y = f(x₁,x₂, … ,x_N)を考えます。すなわち、N個の入力値x₁,x₂, … ,x_Nを与えると、それらに出力値yを対応させるようなルールを考えるということです。数ある関数の中で、特に次のような形で表せる関数を1次関数と呼びます。

y = a₁x₁ + a₂x₂ + ⋯ + a_Nx_N + b　(a₁,a₂, … ,a_N,bは定数)

1次関数は、数ある関数の中で最も扱いやすく、「strong簡単な関数」です。特に、1次関数の「b」以外の部分だけを抜き出した、

a₁x₁ + a₂x₂ + ⋯ + a_Nx_N　(a₁,a₂, … ,a_Nは定数)

の部分をx₁,x₂, … ,x_Nの線形結合（linear combination）と呼びます。つまり、

(x₁,x₂, … ,x_N の1次関数) = (x₁,x₂, … ,x_Nの線形結合) + (定数 b)

です（定数bのことを切片、またはバイアスと呼びます）。

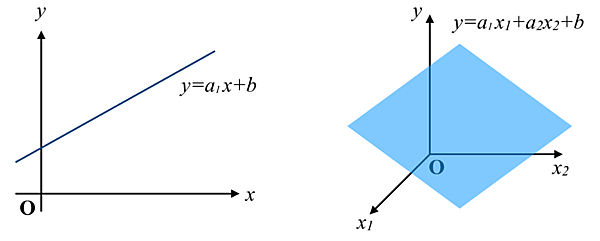
1次関数のグラフは、N = 1のとき以下に示すように直線となり、N = 2のとき平面となります。

1次関数は非常に扱いやすく、良い性質をたくさん持っている関数ですが、我々の周りに現れる関数は、当然ながらこんな簡単な様相をしているわけではありません。

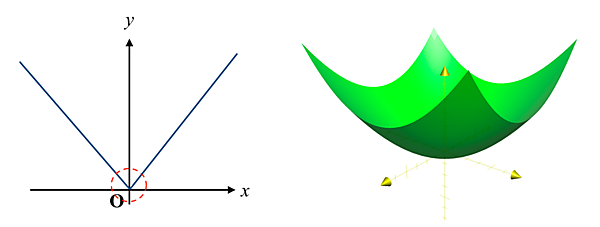
1次関数では表せない関数のことを、我々はまとめてよく非線形であると言います。非線形な関数は「難しい関数」です。次の図に示すグラフのように、非線形な関数はグラフが直線や平面にはなりません（1次関数ではないので当たり前ですね）。

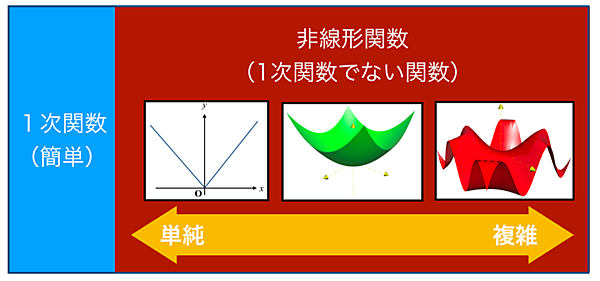
この世界に存在するあらゆる関数は、

・1次関数（最も簡単な関数）
・非線形関数（1次関数ではない関数）

に分けることができます。そして、非線形関数の中にも「比較的単純なもの」から「複雑な様相をあらわすもの」まで、様々なタイプの関数があります。

目標は「複雑な関数の近似」でした

さて、お話を戻しましょう。我々にとっての目標は「関数の近似」でした。前回でも述べたとおり、世の中には複雑な非線形関数が溢れかえっていますが、それを「コンピュータに計算させる」ためには、複雑な関数に対して正確な「近似」を行わなければなりません。そこで、我々は以下のようなアイデアに立ちます。

「複雑な非線形関数」を「たくさんの簡単な関数の組み合わせ」に分解する

直接様子がわからないような複雑な関数をうまく「たくさんの単純な要素に分解」することにより、「簡単な計算に繰り返し」で表現できないか？ということを考えるのです。そこでまず、最初に思いつくだろう以下のアイデアを見てみましょう。

【アイデア①】 複雑な非線形関数を「たくさんの1次関数の組み合わせ」で表す
1次関数は数ある関数の中で最も単純明快な関数なので、「複雑な非線形関数」を「たくさんの1次関数の組み合わせ」に分解できたら、これほど素晴らしいことはありません。

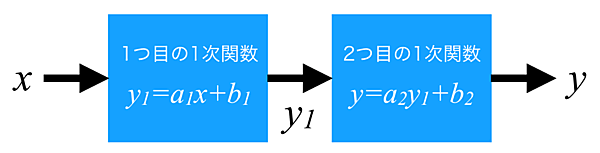
しかし、結論から述べると実はこのアイデアが「不可能」であることは、すぐに分かってしまいます。というのも今、2つの1次関数 y = a₁x + b₁, y = a₂x + b₂があったとき、これらの合成（組み合わせ）を以下のように考えます。

すなわち、

入力xを、

・まず1つめの1次関数 y= a₁x + b₁に入力し、その出力にy₁と名付ける
・今度はそのy₁を2つ目の1次関数 y = a₂x + b₂の入力と考え、入力する
・そのときの出力をyとする

という流れで、最初の入力xに対する最終的な出力yを得るのです。このように「関数を連続して通す」ことにより入力xに対してyが定まるルール（つまり「関数」）を関数の合成（合成関数）と呼びます。我々は今、この「関数の合成」を何度も繰り返すことで、複雑な非線形関数が表せないだろうか？ということを目論んでいるのです。

ところが、この目論みはあっけなく破綻してしまいます。実際にこの「2つの1次関数の合成」の結果を計算してみましょう。まず、1つ目の1次関数の出力は y₁ = a₁x + b₁でした。これを今度は、2つ目の1次関数 y = a₂x + b₂に入力すると…

y = a₂y₁ + b₂ = a₂ (a₁x + b₁) + b₂ = a₁a₂x + a₂b₁ + b₂ = (a₁a₂) x + (a₂b₁ + b₂)

赤字の部分は、定数同士の計算なのでしょせんは定数でしかありません。なので、

A = a₁a₂
B = a₂ b₁ + b₂

とでも置いてしまえば、A、Bは「単なる定数」でしかないのです。

お分かりでしょうか？ 結局、2つの1次関数を合成してできた関数は、再び1次関数

y = A_x + B

の形で書き表せてしまったのです。ここへさらに3つ目、4つ目の1次関数をいくら合成しようが「1次関数と1次関数の合成は1次関数」でしかないことが分かってしまったので、結局「1次関数をいくら合成しようが、1次関数にしかならない」ことがわかります。これでは、1次関数を組み合わせて非線形関数を表現するなんて、できそうにないですね。

【結論】1次関数はどんなに合成しても1次関数にしかならないので、それによって非線形関数を表現することはできない

世の中そんなに甘くはない、ということですね。ですが、まだ諦めません。

【アイデア②】1次関数の間に「単純な非線形関数」を挟んでみる

でも、考えてみればこの結果は当たり前のような気もしませんか? もともと近似したいものは「非線形関数」なのだから、当然その分解には「非線形な要素」が必要なはずで、1次関数だけをたくさん用意しても、そこに「非線形要素」をうまく混ぜない限り近似なんてできるわけがないのです。例えるなら、高級フランス料理を塩と砂糖だけの組み合わせで作ろうとしていたようなものです。たしかに塩と砂糖は単純だし、とても役に立ちますが、いくら何でもありえない! ですよね。

そこで、我々はこんなことを考えます。1次関数の間に「単純な非線形関数」を挟みこむことで、複雑な非線形関数を近似できないか? ということを。

これも結論から言ってしまうと、実はこのアイデアはむちゃくちゃ強力です。というのも、このアイデアを使えば、どんな非線形関数でも（※厳密にはいくつか条件がありますが、ここでは簡単のため触れないことにします）精密に近似できてしまうことが数学的に証明されています（Cybenkoの定理 / 1989）。

すなわち、我々が近似したい「複雑な非線形関数」は、入力を

うまく作った1次関数 ⇒ うまく選んだ単純な非線形関数 ⇒ うまく作った1次関数 ⇒ うまく選んだ単純な非線形関数 ⇒ …

というふうに順番に関数に通してゆけば、原理的には綺麗に表せてしまう（いくらでも精密な近似が可能）のです。これは、なかなか面白いと思いませんか。我々はこの1次関数の間に挟んだ「単純な非線形関数」を活性化関数（activation function）と名付けることにしましょう。

数式だけで書くと大変。そうだ、図解しよう

さて、「関数の近似の仕方」を原理的には理解できた気もしますが、これを「数式だけで表そう」なんて気持ちでいると大変なことになってしまいます。

今、i (i = 1, 2, …) 番目の1次関数を y = a_ix + b_i (i = 1, 2, …) と表し、i ( i = 1, 2, …) 番目の活性化関数を f_i (i = 1, 2, …) と表すことにしましょう。このとき、先程の「1次関数 ⇒ 非線形(活性化)関数 ⇒ …」の流れを数式で表すと次のようになります。

x ⇒ a₁x + b₁ ⇒ f₁ (a₁x + b₁ ) ⇒ a₂f₁ (a₁x + b₁ ) + b₂ ⇒ f₂ (a₂f₁ (a₁x + b₁ ) + b₂ ) ⇒ a₃f₂ (a₂f₁ (a₁x + b₁ ) + b₂ ) + b₃ ⇒ ⋯ ⇒ y

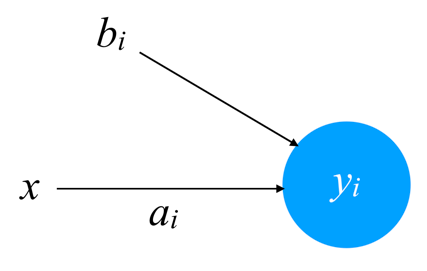
…とてもじゃないですが、数式で書いてなどいられないほど複雑です。そこで、この流れを図で表してみましょう。入力xを1次関数 y = a_ix + b_iに入力するということは、「xにa_iをかけて、それにb_iを足す」ことだと考えることができます。そこで、その様子を以下のように表します。

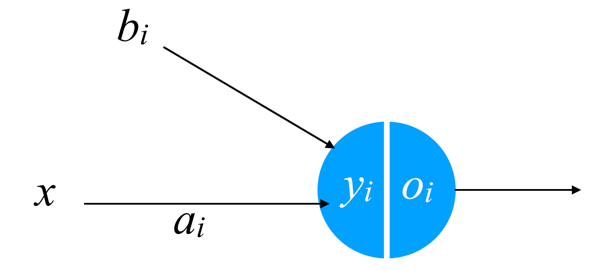
さらに、この次にy_iが活性化関数 f_i を通過して出てきた出力を o_i と表す（o_i = f_i (y_i )です）ことにしたとき、それを次のように表すことにします。

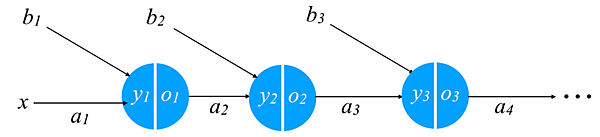
この書き方を使えば、先程の流れは次のように図を使って表すことができます。

お～、何だか見やすくなったのがわかりますね。

今度は、多数の入力x₁,x₂, ⋯ ,x_mに対して出力yを得るような関数についても同様のことを考えてみましょう。流れは、

・入力x₁,x₂,⋯,x_mの1次関数 y_i = a_i,1x₁ + a_i,2x₂ + ⋯ + a_i,mx_m + b_i (i = 1, 2, …) を計算
・1次関数の全出力を適切な活性化関数に通し、その出力をo₁,o₂,⋯ とする
・それらo₁,o₂,⋯の1次関数をまたいくつも（何個でも良い）計算する
・1次関数の全出力を適切な活性化関数に通し、その出力を…（以下同文）

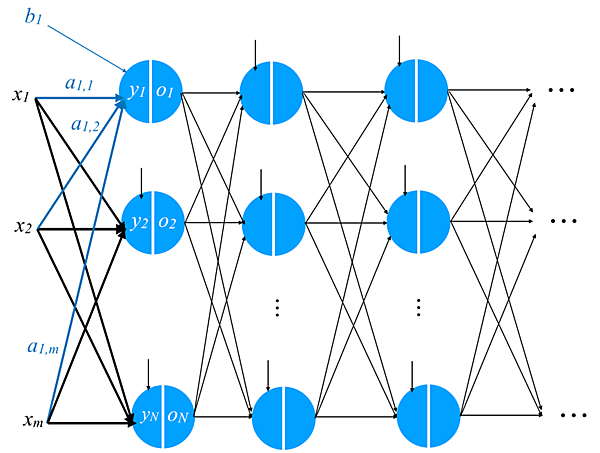
おおっと! 図がぐちゃぐちゃしてきましたが、何もビビる必要はありません。「入力x₁,x₂,⋯,x_mの1次関数をたくさん計算」し、それらを「全て活性化関数に通し」、またそれらの「1次関数をたくさん計算」し、それらをまた「全て活性化関数に通し」…というのを何度も繰り返し、最終的には出力yにたどり着くという、「さっきのアイデア」を図で書いただけです。これ、数式を使って表そうとすると大変なことになってしまうことは先程も見たとおりなので、この「図解」はなかなか良いアイデアだと言えるわけです。

この「図解」は、まるで「点（ノード）」と「辺（エッジ）」が繋がった「ネットワーク」のように見えますね。さらに、入力x₁,x₂,⋯,x_mが1次関数と活性化関数を何度も何度も通りながら、左から右に伝わって行くという「流れ」が見えてきます。実はこの「入力の伝わり方」が脳の神経細胞（ニューロン）を電気信号が伝わってゆく様子に、とても似ている! ということが知られているのです。そのため、我々はこの「入力が1次関数と活性化関数を何度も通って行くことを図解」したこのネットワークをニューラルネットワーク（Neural Network）と呼ぶ（ニューラルというのは「ニューロン的な」といった意味だと思ってください）ことにするわけです。

これが、ニューラルネットワークの「関数近似器の図解」としての導入です。ちょっと難しいところもあったかもしれませんが、突然「脳の神経細胞を電気が伝わるのがこういう感じだから…」という1行説明のすぐ次にニューラルネットワークが出てくるよりも、圧倒的に納得しやすかったことを覚えています。

順伝播と逆伝播

入力がニューラルネットワークを「1次関数と活性化関数を順に通りながら」伝わっていくことを順伝播（forward propagation）と呼びます。

ところで、皆さんももしかしたら気になっていたかもしれませんが、実は今までの議論には「ひとつ見て見ぬふりをしている重要なこと」があります。それは…

1次関数を「うまく作る」とか、活性化関数を「うまく選ぶ」とかさっきからずっと言ってるけど、それ、そもそもどうやって「選」べば良いの?

これはすごく重要な問題です。その「うまい」作り方や選び方がわからないと、我々はうまく「近似」できませんから。

ところが、実は我々は実際の「入力と正しい出力のペア（教師データ）」をいくつも用意し、それを用いて１次関数の「適切な選び方」を自動的に求められてしまうのです。この具体的な方法（アルゴリズム）を誤差逆伝播法（back propagation algorithm）と呼びます。ニューラルネットワークにたくさん実際のデータを見せて、少しずつ1次関数の「適切な選び方」が自動的に定まってゆく…まるで、これは人間の脳が実際に見聞きした情報によりどんどん「正しく」書き換えられて行き、何かを学んでいるようですね。そのため、これをニューラルネットワークの「学習」と呼ぶのです。

こんなふうに、「関数近似器」の視点で、ニューラルネットワークを導入してみました。では、このニューラルネットワークは、どうやって「学習」をするのでしょうか? それはまた、次回以降のお楽しみ。