線型代数への招待

はじめに

前回は、具体的なニューラルネットワークを題材に、バックプロパゲーションというアルゴリズムを紹介しました。連鎖律の原理という強力な偏微分の法則を用いて、出力層から入力層に向かって上手く誤差を伝播できましたね。

今回からは、機械学習・深層学習の分野で頻出の「線型代数」の世界をもっと深く覗いていきます。これまでもベクトルや行列といった内容には触れてきましたが、ここで改めて理解を定着させましょう。今回の記事を読んでいく途中、きっと意外なことに気づくはずです。

線型って? 代数って?

突然ですが、線型代数という言葉の意味はご存知ですか。線型代数は英語でlinear algebraといい、linearが線型で、algebraが代数という意味に対応します。

ここでいう線型とは「原点を通る直線(及びその直線が持つ性質)」のことです。一方の「代数」は非常にざっくり言うと「$x$や$A$といった文字変数を用いて、足し算や掛け算を考えたり、方程式を解いたりする」ことです。要するに、線型代数とは直線を表す式を用意して方程式を解くという学問なのです(ちなみに線型代数のことを線型代数と表記することもありますが、どちらも同じです)。

では、この線型代数という学問が機械学習・深層学習の分野でどのように利用されているのかを見ていきます。

内積という最強の表記

さて深層学習の例と言えば、これですね。ニューロンに登場してもらいましょう。

このニューロンの入出力の関係を表す式はどのようになるでしょうか。これまで何度も出てきたので大丈夫ですよね。正解は、次のようになります(式1)。

$$y=w_0∙1 + w_1∙x_1 + w_2∙x_2 + w_3∙x_3 + w_4∙x_4$$

入力の値に重みが掛け算されることがポイントでしたね。

さて、この式ですが、皆さんこれを見てどのように思いますか。「文字が多い」「添字を間違えそう」など色々とあると思いますが、私は素直に「長い！」と思ってしまいます。どうにかして、もっとシンプルに書けないでしょうか。ということで、この式をじっと見てみます。

そうすると、思い当たるものがありませんか。「あれ、これは内積の形に似ている!?」その通りです。これまでに学んだ通り$w = (w_0, w_1, w_2, w_3, w_4)$、$x =(1, x_1, x_2, x_3, x_4)$と２つのベクトルを定めると、この式1は

$$y = w_0∙1 + w_1∙x_1 + w_2∙x_2 + w_3∙x_3 + w_4∙x_4 = w∙x = w^Tx$$

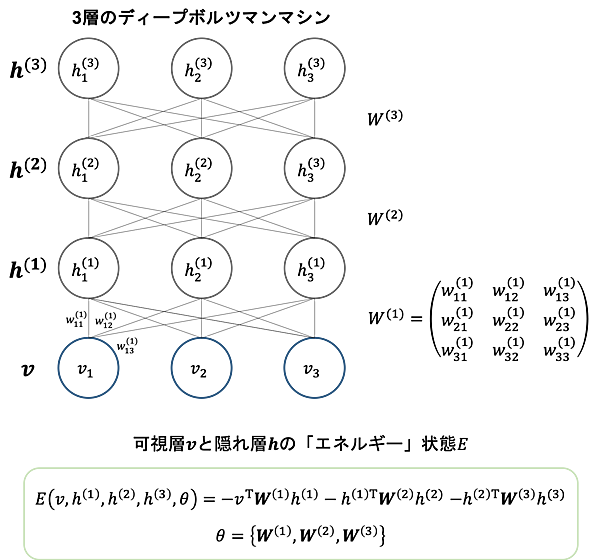
別の例を見て見ましょう。下図は(著者が大好きな)ディープボルツマンマシンと呼ばれる機械学習モデルです(ボルツマンマシンについて詳しく知りたい方は、是非色々と調べてみてください。理論的には非常に難しい組み合わせ問題を解くことができる夢のようなモデルです)。何やらニューロン間の結合がごちゃごちゃしていますが、ベクトルと行列を用いることでネットワークの構造をシンプルに表現できています。

また、ボルツマンマシンにはエネルギーという概念がありますが、こちらもベクトルと行列の積で簡潔に表現できています。数式の詳しいことが分からなくても構いません。大切なのは「変数が沢山ありそうなのに、こんなにも簡単に記述できる」という点です。

ここで非常に重要な気づきが得られます。それは「私たちは今までの過程で線型代数の言葉の意味を意識しただろうか？」ということです。文字変数を使ったぐらいで、正直なところあまり意識していませんね。この事実は機械学習・深層学習における線型代数の立ち位置を端的に表しています。すなわちこれらの分野において線型代数は

ということなのです。見た目を簡単にするためにだけに線型代数という学問が必要というのは少し意外かもしれませんね。もちろん線型代数の深い知識を必要とすることもありますが(例えば、固有値・固有ベクトルなど)、表記としての線型代数を知っているだけでも機械学習・深層学習の世界を十分理解できるのです。

なんだかちょっと煙に包まれた？と感じた人のために

ここまでの説明で少し腑に落ちない方もいるかもしれません。「機械学習・深層学習において線型代数の意義は、見た目をシンプルにすることだって？言っている意味は分かるけれど、数学ってなんかもっと高貴(？)な目的のために作られたものじゃないの？見た目を綺麗にまとめるためだけに数学の一分野が登場するなんて、なんだか胡散臭い！」と思ったりしませんでしたか(思わない)？しかし、著者自身こういった質問をよく受けます。

著者は決して数学の著名な学者ではありません。ただ、それでもこれまで約20年間数学に携わってきて、1つだけ確かに実感できることがあります。それは「数学とは言語そのものである」ということです。ビジネスにおけるコミュニケーションにおいても、伝えたい内容を要約し、結論やその理由、および具体例などに分解したりすると思います。それは数学でも一緒なのです。

今回の例で言うと、式1を式2の形に変形することで、出力$y$が2つのベクトル$w$及び$x$によって完全に決定されることが即座に分かります。また、$x$と$y$のデータセットを所持している時、$y = w^Tx$は$w$についての連立方程式に帰着し、線型代数のテクニックで解を求められるようになります。こういった例から「線型代数という数学の力を借りれば表記が簡潔になる」こと自体に価値があると分かります。そして「簡潔になったからこそ分かることがあり、議論できることがある」と言うことも実感できます。

人間の「視覚」には得意・不得意があり、人間の「手計算力」にも限界があります(例えば、ベクトルを使わずに1000個の変数を書き並べることは難しく、かつ生産性がない)。人間はそこで立ち止まることなく、築き上げたその数学力で現状を打破しようとしてきました。その一例が「表記としての線型代数」なのだと著者は考えています。

おわりに

今回は機械学習・深層学習の線型代数の立ち位置に焦点を当ててみました。後半多少私の気持ちが入り込んでしまいましたが、「記述をシンプルにできる！」ということ自体に価値を感じていただければと思います(とは言うものの、今後少し難しい線型代数のコンテンツもご用意していますので、お楽しみに)。

次回は、今回も少し登場した「線型代数の力を使って連立方程式と解く」ことに着目してみます。